Regression Discontinuity: Part II
Outline for Today
- Revisit MA Data with Star Ratings
- Basic RD with Star Ratings
- Manipulation and Balance Checks
- Effects Across Ratings
Medicare Advantage Star Ratings Data
Revisit Data Import
Enrollments and star ratings
| (1) | |
|---|---|
| (Intercept) | 0.026 |
| (0.003) | |
| Star Rating = 2 | 0.025 |
| (0.003) | |
| Star Rating = 2.5 | 0.070 |
| (0.003) | |
| Star Rating = 3 | 0.043 |
| (0.003) | |
| Star Rating = 3.5 | 0.030 |
| (0.003) | |
| Star Rating = 4 | 0.030 |
| (0.004) | |
| Star Rating = 4.5 | 0.029 |
| (0.005) | |
| Num.Obs. | 22537 |
| R2 | 0.045 |
Problems
- Certainly not the effect of quality disclosure
- Lots of things unobserved, like
- actual quality
- perceived quality
- prices
Regression Discontinuity with Star Ratings
Note about scores
CMS does more than just an average…
- variance across individual metrics
- high variance is punished, low variance rewarded
- Part C and D scores combined for online reporting (not relevant for 2009)
- For our setting, we’ll just drop contracts that don’t seem to match our strategy very well, but in practice, you’d want to recreate the star ratings much more closely
Data Cleanup
We need contracts where the raw rating maps cleanly to the displayed star rating. CMS rounds raw scores to the nearest half-star, so a raw rating of 2.25 is the threshold between 2.0 and 2.5 stars.
- Keep contracts with Star Rating of 2.0 or 2.5
- Drop contracts where raw_rating doesn’t match the assigned star (likely due to CMS adjustments we can’t replicate)
Data Cleanup (code)
# Candidates: partc_score 2 or 2.5 with non-missing raw_rating and partc_score
ma_25star_candidates <- ma_2009 %>%
filter(
!is.na(raw_rating),
!is.na(partc_score),
Star_Rating %in% c(2.0, 2.5)
)
n_candidates_total <- nrow(ma_25star_candidates)
n_candidates_by_score <- ma_25star_candidates %>% count(partc_score)
# Final sample: raw_rating in the range consistent with the star score
ma_25star <- ma_25star_candidates %>%
filter(
raw_rating >= 2,
raw_rating <= 2.5,
(raw_rating >= 2.25 & Star_Rating == 2.5) | (raw_rating < 2.25 & Star_Rating == 2)
)
n_25star_total <- nrow(ma_25star)
n_25star_by_score <- ma_25star %>% count(partc_score)# Candidates: partc_score 2 or 2.5 with non-missing raw_rating and partc_score
candidates_mask = (
ma_2009["raw_rating"].notna()
& ma_2009["Star_Rating"].notna()
& ma_2009["Star_Rating"].isin([2.0, 2.5])
)
ma_25star_candidates = ma_2009.loc[candidates_mask].copy()
n_candidates_total = len(ma_25star_candidates)
n_candidates_by_score = ma_25star_candidates["Star_Rating"].value_counts()
# Final sample: raw_rating in the range consistent with the star score
match_mask = (
ma_25star_candidates["raw_rating"].between(2, 2.5)
& (
((ma_25star_candidates["Star_Rating"] == 2.5) &
(ma_25star_candidates["raw_rating"] >= 2.25))
|
((ma_25star_candidates["Star_Rating"] == 2) &
(ma_25star_candidates["raw_rating"] <= 2.25))
)
)
ma_25star = ma_25star_candidates.loc[match_mask].copy()
n_25star_total = len(ma_25star)
n_25star_by_score = ma_25star["Star_Rating"].value_counts()
print("Obs with partc_score 2 or 2.5:", n_candidates_total)
print(n_candidates_by_score)
print("Obs with raw_rating in the matching range:", n_25star_total)
print(n_4star_by_score)Obs with partc_score 2 or 2.5: 12127 # A tibble: 2 × 2
partc_score n
<dbl> <int>
1 2 4545
2 2.5 7582Obs with raw_rating in the matching range: 6935 # A tibble: 2 × 2
partc_score n
<dbl> <int>
1 2 4303
2 2.5 2632Binned Scatterplot
rd.result <- rdplot(ma_25star$mkt_share, ma_25star$raw_rating,
c=2.25, p=2,
title="RD Plot with Binned Average",
x.label="Running Variable",
y.label="Outcome",
hide = TRUE)
bin.avg <- as_tibble(rd.result$vars_bins)
plot.bin <- bin.avg %>% ggplot(aes(x=rdplot_mean_x,y=rdplot_mean_y)) +
geom_point() + theme_bw() +
geom_vline(aes(xintercept=2.25),linetype='dashed') +
scale_x_continuous(
breaks = c(2, 2.125, 2.25, 2.375, 2.5),
label = c("2.0", "2.125", "2.25", "2.375", "2.5")
) +
xlab("Raw Rating") + ylab("Market Share") +
annotate("text", x=2.25, y=Inf, label="2.5-star\ncutoff",
vjust=1.5, hjust=-0.1, size=3.5, color="grey40")import pandas as pd
import matplotlib.pyplot as plt
from rdrobust import rdplot
# RD plot using mkt_share as outcome and raw_rating as running variable
rd_result = rdplot(
y=ma_25star["mkt_share"].values,
x=ma_25star["raw_rating"].values,
c=2.25,
title="RD Plot with Binned Average",
x_label="Running Variable",
y_label="Outcome",
hide=True # don't show the built-in plot
)
# vars_bins is already a pandas DataFrame in the Python implementation
bin_avg = rd_result.vars_bins
# Recreate the custom plot
fig, ax = plt.subplots()
ax.scatter(
bin_avg["rdplot_mean_x"],
bin_avg["rdplot_mean_y"]
)
ax.axvline(x=2.25, linestyle="--", color="grey")
ax.set_xticks([2.0, 2.125, 2.25, 2.375, 2.5])
ax.set_xticklabels(["2.0", "2.125", "2.25", "2.375", "2.5"])
ax.set_xlabel("Raw Rating")
ax.set_ylabel("Market Share")
ax.set_title("RD Plot with Binned Average")
ax.annotate("2.5-star\ncutoff", xy=(2.25, ax.get_ylim()[1]),
xytext=(2.27, ax.get_ylim()[1]*0.95), fontsize=9, color="grey")
plt.tight_layout()
plt.show()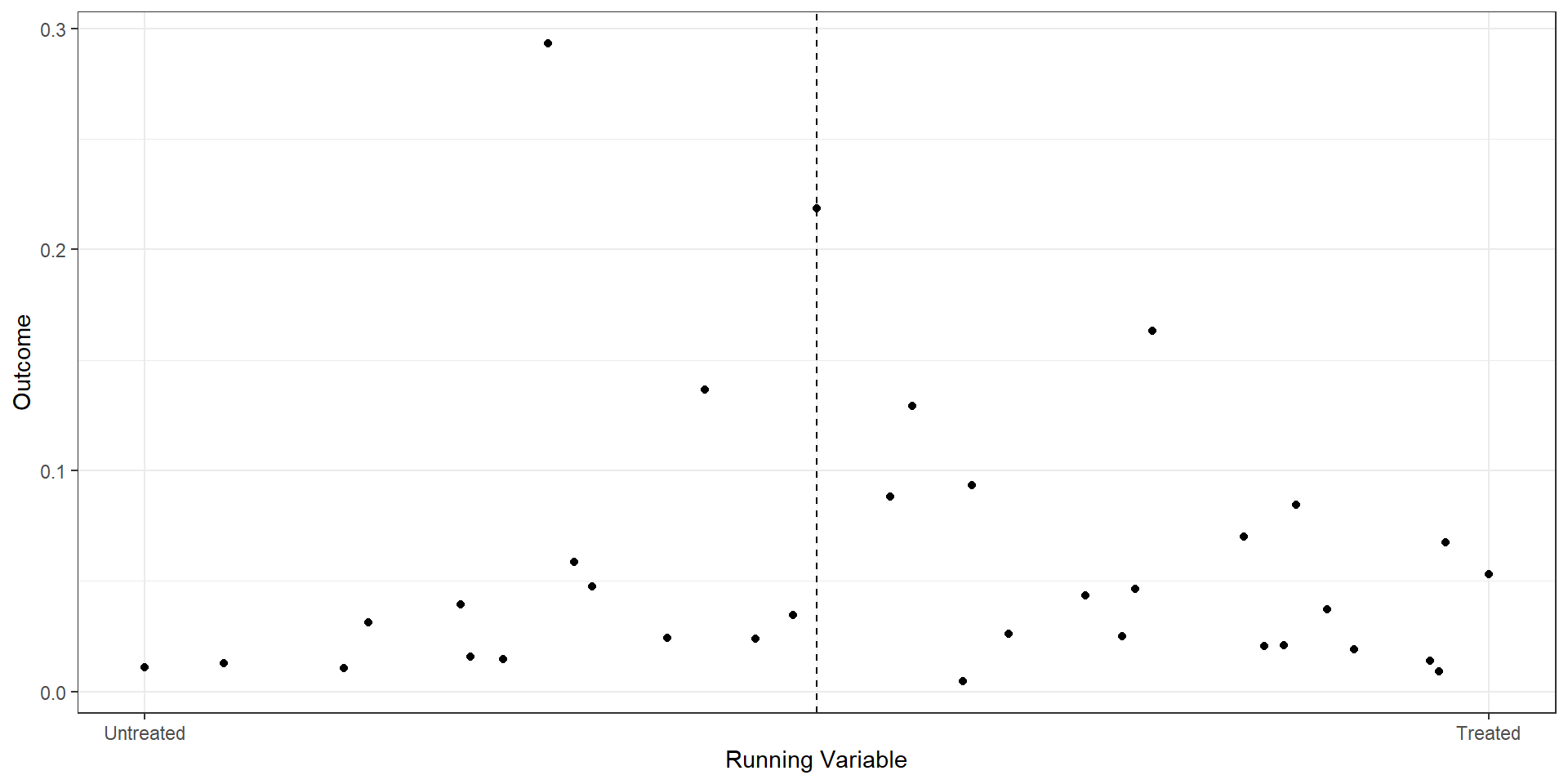
RD from OLS
ma.rd1 <- ma_25star %>%
mutate(score = raw_rating - 2.25,
treat = (score>=0),
window1 = (score>=-.175 & score<=.175),
window2 = (score>=-.125 & score<=.125),
score_treat=score*treat)
star25.1 <- lm(mkt_share ~ score + treat, data=ma.rd1)
star25.2 <- lm(mkt_share ~ score + treat, data= (ma.rd1 %>% filter(window1==TRUE)))
star25.3 <- lm(mkt_share ~ score + treat + score_treat, data= (ma.rd1 %>% filter(window1==TRUE)))
star25.4 <- lm(mkt_share ~ score + treat + score_treat, data= (ma.rd1 %>% filter(window2==TRUE)))
est1 <- as.numeric(star25.1$coef[3])
est2 <- as.numeric(star25.2$coef[3])
est3 <- as.numeric(star25.3$coef[3])
est4 <- as.numeric(star25.4$coef[3])
rows <- tribble(~term, ~ m1, ~ m2, ~ m3 , ~ m4,
'Bandwidth', "0.25", "0.175", "0.175", "0.125")
attr(rows, 'position') <- 7import pandas as pd
import statsmodels.formula.api as smf
# Start from ga_ma_4star DataFrame
ma_rd1 = ma_25star.copy()
ma_rd1["score"] = ma_rd1["raw_rating"] - 2.25
ma_rd1["treat"] = (ma_rd1["score"] >= 0).astype(int)
ma_rd1["window1"] = (ma_rd1["score"].between(-0.175, 0.175))
ma_rd1["window2"] = (ma_rd1["score"].between(-0.125, 0.125))
ma_rd1["score_treat"] = ma_rd1["score"] * ma_rd1["treat"]
# Regressions
star25_1 = smf.ols("mkt_share ~ score + treat", data=ma_rd1).fit()
star25_2 = smf.ols("mkt_share ~ score + treat",
data=ma_rd1[ma_rd1["window1"]]).fit()
star25_3 = smf.ols("mkt_share ~ score + treat + score_treat",
data=ma_rd1[ma_rd1["window1"]]).fit()
star25_4 = smf.ols("mkt_share ~ score + treat + score_treat",
data=ma_rd1[ma_rd1["window2"]]).fit()
# Extract treatment effect (coefficient on treat)
est1 = float(star25_1.params["treat"])
est2 = float(star25_2.params["treat"])
est3 = float(star25_3.params["treat"])
est4 = float(star25_4.params["treat"])
# Bandwidth row (analogous to tribble + attribute)
rows = pd.DataFrame(
{
"term": ["Bandwidth"],
"m1": ["0.25"],
"m2": ["0.175"],
"m3": ["0.175"],
"m4": ["0.125"],
}
)
rows.attrs["position"] = 7| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Raw Score | 0.010 | -0.277 | -0.141 | -0.204 |
| (0.021) | (0.038) | (0.050) | (0.054) | |
| Treatment | 0.012 | 0.058 | 0.066 | 0.070 |
| (0.006) | (0.008) | (0.008) | (0.010) | |
| Score x Treat | -0.328 | -0.255 | ||
| (0.078) | (0.117) | |||
| Bandwidth | 0.25 | 0.175 | 0.175 | 0.125 |
| Num.Obs. | 6935 | 4605 | 4605 | 4422 |
| R2 | 0.009 | 0.012 | 0.016 | 0.013 |
Interpretation
- OLS on full sample: 1.2% increase in market share for 2.5-star versus 2.0-star plans
- RD on 0.175 bandwidth: 5.8% increase when imposing constant slopes, 6.6% increase when allowing for differential slopes
- RD on 0.125 bandwidth: 7% increase (again allowing for differential slopes)
Built-in RD packages
from rdrobust import rdrobust
# Fixed bandwidth
est1 = rdrobust(
y=ma_rd1["mkt_share"].values,
x=ma_rd1["score"].values,
c=0,
h=0.125,
p=1,
kernel="uniform",
vce="hc0",
masspoints="off",
)
# Optimal bandwidth (letting rdrobust choose h)
estopt = rdrobust(
y=ma_rd1["mkt_share"].values,
x=ma_rd1["score"].values,
c=0,
p=1,
kernel="uniform",
vce="hc0",
masspoints="off",
)| Spec | Estimate | Robust CI | BW | N |
|---|---|---|---|---|
| Fixed (h=0.125) | 0.0701 | [0.1506, 0.2952] | 0.125 | 6935 |
| Optimal | 0.1809 | [0.0957, 0.3062] | 0.033 | 6935 |
Manipulation and Balance Checks
Manipulation of the running variable
from rdrobust import rddensity, rdplotdensity
import matplotlib.pyplot as plt
# Run McCrary-style density test at cutoff 0
dens1 = rddensity(x=ma_rd1["score"].values, c=0)
# Create the density plot object (rdplotdensity returns a matplotlib figure/axes)
densplot = rdplotdensity(dens1, x=ma_rd1["score"].values)
# If you want to explicitly show or tweak:
fig = densplot["fig"]
ax = densplot["ax"]
ax.set_title("Density test around cutoff")
ax.set_xlabel("Score")
ax.set_ylabel("Estimated density")
plt.show()| Value | |
|---|---|
| T-statistic | 55.91 |
| P-value | 0.00 |
Interpretation: A large p-value means we cannot reject equal density on both sides of the cutoff, which is what we want. No evidence of manipulation.
Covariate balance
import numpy as np
import pandas as pd
from sklearn.neighbors import NearestNeighbors
import matplotlib.pyplot as plt
# 1. Subset data as in your R code
sub = (
ma_rd1
.loc[
(ma_rd1["window2"]) &
ma_rd1["treat"].notna() &
ma_rd1["premium_partc"].notna() &
ma_rd1["ma_rate"].notna()
]
.copy()
)
covariates = ["premium_partc", "ma_rate"]
X = sub[covariates].to_numpy()
t = sub["treat"].astype(int).to_numpy()
# 2. Mahalanobis nearest-neighbor matching (1:1)
# Estimate covariance matrix of covariates and its inverse
V = np.cov(X, rowvar=False)
V_inv = np.linalg.inv(V)
# Fit NN on controls only
nn = NearestNeighbors(
n_neighbors=1,
metric="mahalanobis",
metric_params={"V": V}
)
nn.fit(X[t == 0])
# For each treated unit, find nearest control
dist, idx = nn.kneighbors(X[t == 1])
control_matches = sub.loc[t == 0].iloc[idx[:, 0]].copy()
treated_matched = sub.loc[t == 1].copy()
# Build matched sample
matched = pd.concat(
[
treated_matched.reset_index(drop=True),
control_matches.reset_index(drop=True)
],
axis=0
).reset_index(drop=True)
matched["treat"] = np.r_[np.ones(len(treated_matched)), np.zeros(len(control_matches))]
# 3. Function for standardized mean differences (SMD)
def smd(df, var, treat_col="treat"):
g1 = df[df[treat_col] == 1][var]
g0 = df[df[treat_col] == 0][var]
m1, m0 = g1.mean(), g0.mean()
s = np.sqrt(0.5 * (g1.var(ddof=1) + g0.var(ddof=1)))
return (m1 - m0) / s
# SMDs before and after matching
smd_before = [smd(sub, v) for v in covariates]
smd_after = [smd(matched, v) for v in covariates]
# 4. “Love plot” (absolute SMDs)
fig, ax = plt.subplots()
y_pos = np.arange(len(covariates))
ax.scatter(np.abs(smd_before), y_pos, marker="o", label="Unmatched")
ax.scatter(np.abs(smd_after), y_pos, marker="s", label="Matched")
ax.set_yticks(y_pos)
ax.set_yticklabels(covariates)
ax.set_xlabel("Absolute standardized mean difference")
ax.axvline(0.1, linestyle="--") # common reference line
ax.legend()
ax.invert_yaxis() # to mimic cobalt’s ordering
plt.tight_layout()
plt.show()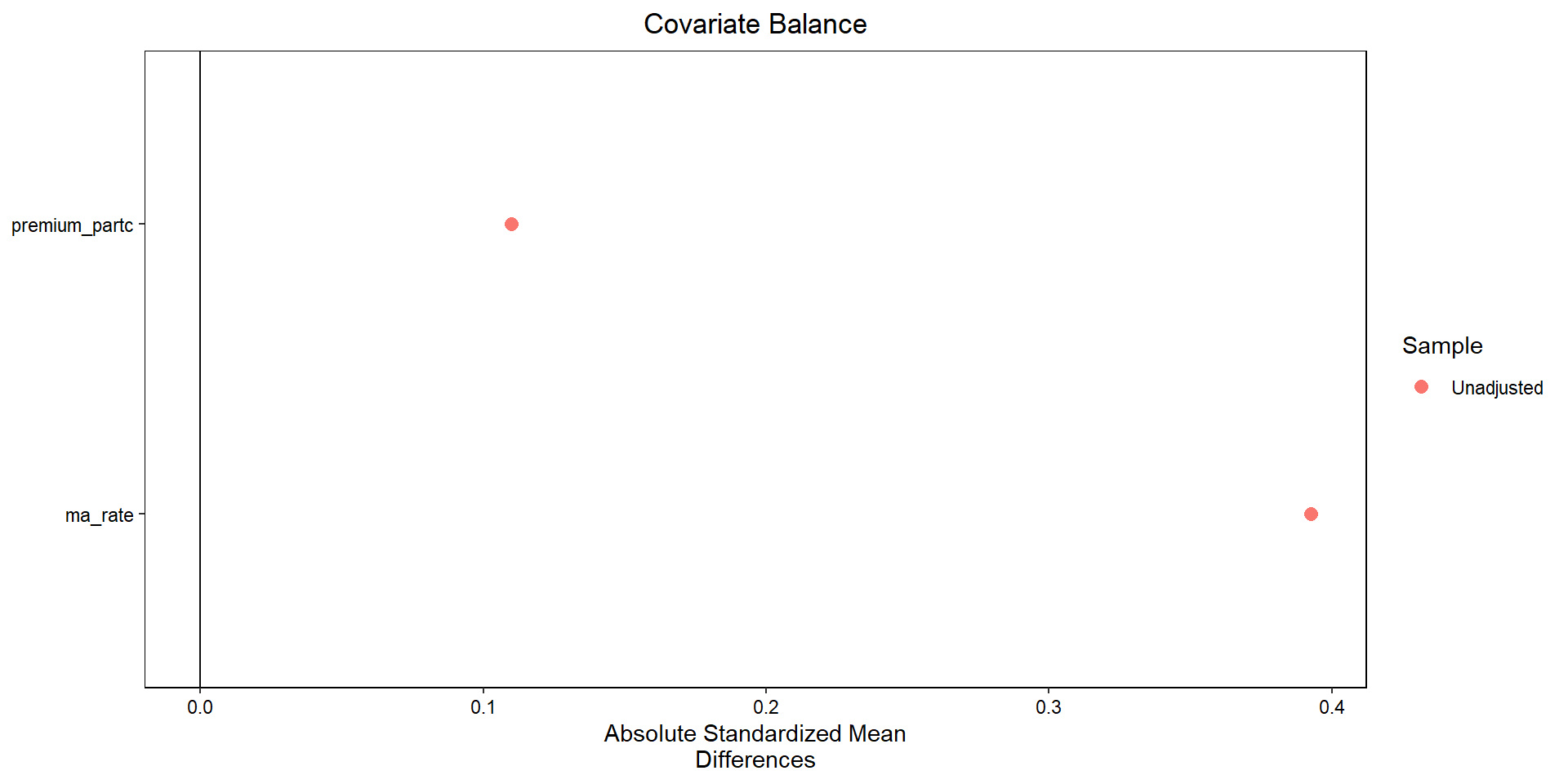
Effects across Rating Thresholds
Effects for 2.5 versus 2.0 Stars
ma.rd225 <- ma_2009 %>%
filter(Star_Rating==2 | Star_Rating==2.5) %>%
mutate(score = raw_rating - 2.25,
treat = (score>=0),
window1 = (score>=-.175 & score<=.175),
window2 = (score>=-.125 & score<=.125),
score_treat=score*treat)
est225 <- rdrobust(y=ma.rd225$mkt_share, x=ma.rd225$score, c=0,
h=0.125, p=1, kernel="uniform", vce="hc0",
masspoints="off")import pandas as pd
from py_rdpackages import rdrobust # wrapper around rdrobust in R
# starting from ma_2009 as a pandas DataFrame
ma_rd225 = (
ma_2009
.loc[ma_2009["Star_Rating"].isin([2, 2.5])]
.assign(
score=lambda d: d["raw_rating"] - 2.25,
treat=lambda d: (d["score"] >= 0).astype(int),
window1=lambda d: d["score"].between(-0.175, 0.175),
window2=lambda d: d["score"].between(-0.125, 0.125),
score_treat=lambda d: d["score"] * d["treat"],
)
)
est225 = rdrobust(
y=ma_rd225["mkt_share"].to_numpy(),
x=ma_rd225["score"].to_numpy(),
c=0,
h=0.125,
p=1,
kernel="uniform", # if this errors, try kernel="uni"
vce="hc0",
masspoints="off"
)| Spec | Estimate | Robust CI | BW | N |
|---|---|---|---|---|
| 2.5 vs 2.0 (h=0.125) | 0.0701 | [0.1506, 0.2952] | 0.125 | 12127 |
Effects across all thresholds
Same approach, applied to every half-star cutoff. The code below loops over each threshold and collects the rdrobust estimates into a single data frame.
cutoffs <- tibble(
lower = c(2, 2.5, 3, 3.5),
upper = c(2.5, 3, 3.5, 4),
cutoff = c(2.25, 2.75, 3.25, 3.75)
)
rd_results <- cutoffs %>%
pmap_dfr(function(lower, upper, cutoff) {
dat <- ma_2009 %>%
filter(Star_Rating == lower | Star_Rating == upper) %>%
mutate(score = raw_rating - cutoff)
est <- rdrobust(y=dat$mkt_share, x=dat$score, c=0,
h=0.125, p=1, kernel="uniform", vce="hc0",
masspoints="off")
tibble(
threshold = paste0(upper, " vs ", lower),
estimate = est$coef[2],
ci_lower = est$ci[3,1],
ci_upper = est$ci[3,2],
n = est$N[1] + est$N[2]
)
})from rdrobust import rdrobust
import pandas as pd
cutoffs = [
(2, 2.5, 2.25),
(2.5, 3, 2.75),
(3, 3.5, 3.25),
(3.5, 4, 3.75),
]
results = []
for lower, upper, cutoff in cutoffs:
dat = ma_2009[ma_2009["Star_Rating"].isin([lower, upper])].copy()
dat["score"] = dat["raw_rating"] - cutoff
est = rdrobust(
y=dat["mkt_share"].values,
x=dat["score"].values,
c=0, h=0.125, p=1,
kernel="uniform", vce="hc0",
masspoints="off"
)
results.append({
"threshold": f"{upper} vs {lower}",
"estimate": est.coef.iloc[1, 0], # bias-corrected
"ci_lower": est.ci.iloc[2, 0], # robust CI
"ci_upper": est.ci.iloc[2, 1],
})
rd_results = pd.DataFrame(results)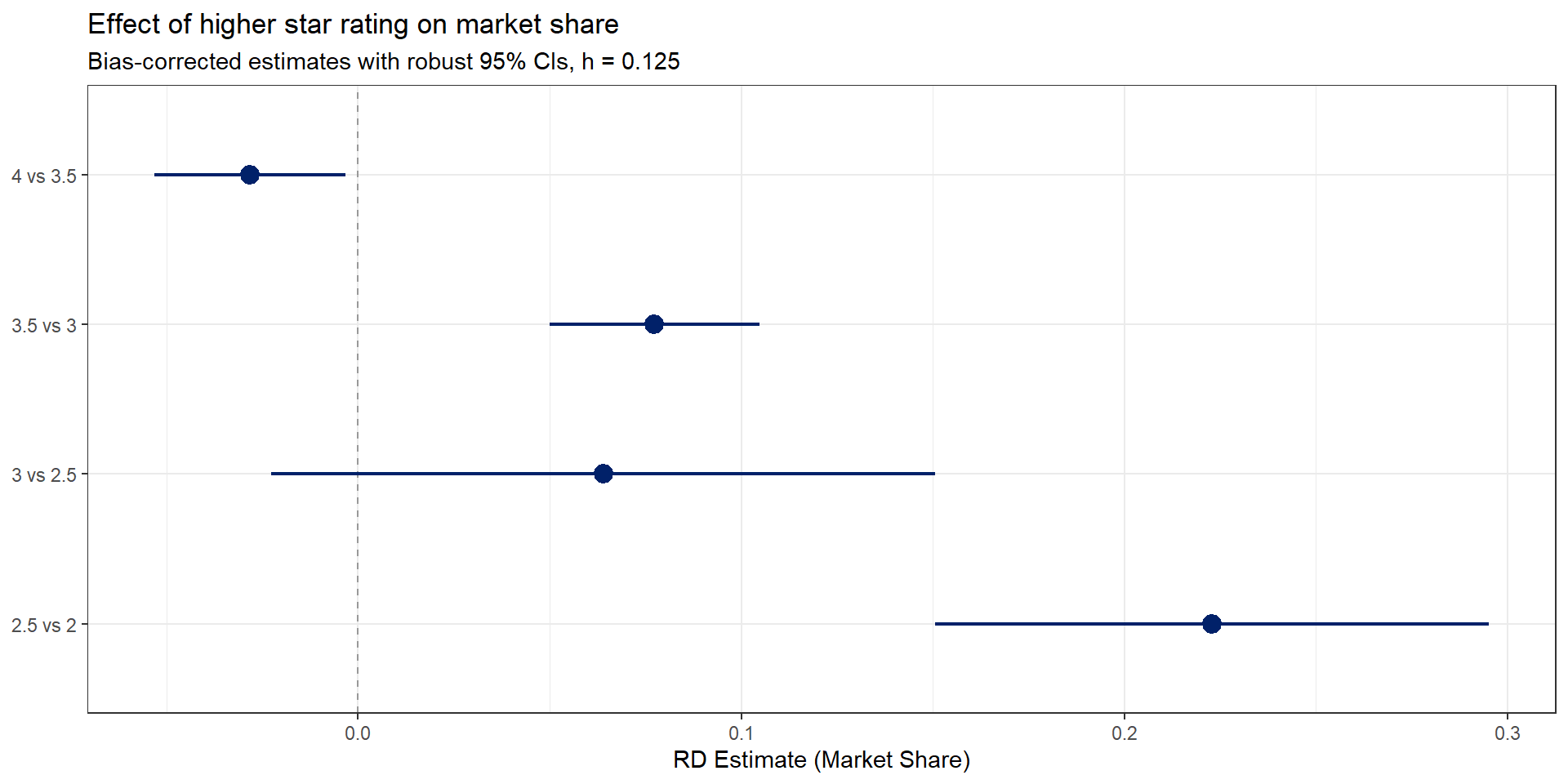
What do we see?
- Largest effects at the lower end of the star rating distribution (2.5 vs 2.0)
- Effects shrink and become noisier at higher thresholds
- Consistent with consumers responding more to quality signals when baseline quality is low
A note on discrete running variables
Star ratings are discrete (only a few unique values of the running variable). Standard RD asymptotics assume a continuous running variable, so we need adjustments.
- Fewer mass points means less variation near the cutoff.
rdrobusthas amasspointsoption to handle this. - Local randomization: if we believe assignment is as-good-as-random between adjacent mass points, we can use randomization inference instead of large-sample asymptotics.
- Fisher’s exact test: test the sharp null of no treatment effect by permuting treatment labels among units near the cutoff.
See Cattaneo, Idrobo, and Titiunik (2020), Chapter 4 for details.