Instrumental Variables: Part I

Ian McCarthy | Emory University

Outline for Today

Introduction to Instrumental Variables
IV Assumptions
IV with Simulated Data
Interpreting IV Estimates

Introduction to Instrumental Variables

What is instrumental variables

Instrumental Variables (IV) is a way to identify causal effects using variation in treatment particpation that is due to an exogenous variable that is only related to the outcome through treatment.

Why bother with IV?

Two reasons to consider IV:

Selection on unobservables
Reverse causation

Either problem is sometimes loosely referred to as endogeneity

Simple example

Consider simple regression equation: \[y = \beta x + \varepsilon (x),\] where \(\varepsilon(x)\) reflects the dependence between our observed variable and the error term.

Simple OLS will yield \[\frac{dy}{dx} = \beta + \frac{d\varepsilon}{dx} \neq \beta\]

What does IV do?

The regression we want to do, \[y_{i} = \alpha + \delta D_{i} + \gamma A_{i} + \epsilon_{i},\] where \(D_{i}\) is treatment (think of schooling for now) and \(A_{i}\) is something like ability.
\(A_{i}\) is unobserved, so instead we run \[y_{i} = \alpha + \beta D_{i} + \epsilon_{i}\]
From this “short” regression, we don’t actually estimate \(\delta\). Instead, we get an estimate of \[\beta = \delta + \lambda_{ds}\gamma \neq \delta,\] where \(\lambda_{ds}\) is the coefficient of a regression of \(A_{i}\) on \(D_{i}\).

Intuition

IV will recover the “long” regression without observing underlying ability

IF our IV satisfies all of the necessary assumptions.

More formally

We want to estimate \[E[Y_{i} | D_{i}=1] - E[Y_{i} | D_{i}=0]\]
With instrument \(Z_{i}\) that satisfies relevant assumptions, we can estimate this as \[E[Y_{i} | D_{i}=1] - E[Y_{i} | D_{i}=0] = \frac{E[Y_{i} | Z_{i}=1] - E[Y_{i} | Z_{i}=0]}{E[D_{i} | Z_{i}=1] - E[D_{i} | Z_{i}=0]}\]
In words, this is effect of the instrument on the outcome (“reduced form”) divided by the effect of the instrument on treatment (“first stage”)

Derivation

Recall “long” regression: \(Y=\alpha + \delta S + \gamma A + \epsilon\).

\[\begin{align} COV(Y,Z) & = E[YZ] - E[Y] E[Z] \\ & = E[(\alpha + \delta S + \gamma A + \epsilon)\times Z] - E[\alpha + \delta S + \gamma A + \epsilon)]E[Z] \\ & = \alpha E[Z] + \delta E[SZ] + \gamma E[AZ] + E[\epsilon Z] \\ & \hspace{.2in} - \alpha E[Z] - \delta E[S]E[Z] - \gamma E[A] E[Z] - E[\epsilon]E[Z] \\ & = \delta (E[SZ] - E[S] E[Z]) + \gamma (E[AZ] - E[A] E[Z]) \\ & \hspace{.2in} + E[\epsilon Z] - E[\epsilon] E[Z] \\ & = \delta C(S,Z) + \gamma C(A,Z) + C(\epsilon, Z) \end{align}\]

Derivation

Working from \(COV(Y,Z) = \delta COV(S,Z) + \gamma COV(A,Z) + COV(\epsilon,Z)\), we find

\[\delta = \frac{COV(Y,Z)}{COV(S,Z)}\]

if \(COV(A,Z)=COV(\epsilon, Z)=0\)

IVs in practice

Easy to think of in terms of randomized controlled trial…

Measure	Offered Seat	Not Offered Seat	Difference
Score	-0.003	-0.358	0.355
% Enrolled	0.787	0.046	0.741
Effect			0.48

Angrist et al., 2012. “Who Benefits from KIPP?” Journal of Policy Analysis and Management.

What is IV really doing

Think of IV as two-steps:

Isolate variation due to the instrument only (not due to endogenous stuff)
Estimate effect on outcome using only this source of variation

In regression terms

Interested in estimating \(\delta\) from \(y_{i} = \alpha + \beta x_{i} + \delta D_{i} + \varepsilon_{i}\), but \(D_{i}\) is endogenous (no pure “selection on observables”).

Step 1: With instrument \(Z_{i}\), we can regress \(D_{i}\) on \(Z_{i}\) and \(x_{i}\): \[D_{i} = \lambda + \theta Z_{i} + \kappa x_{i} + \nu,\] and form prediction \(\hat{D}_{i}\).
Step 2: Regress \(y_{i}\) on \(x_{i}\) and \(\hat{D}_{i}\): \[y_{i} = \alpha + \beta x_{i} + \delta \hat{D}_{i} + \xi_{i}\]

Derivation

Recall our first-stage, \(S=\theta Z + \varepsilon\), where \(\hat{\theta}=\frac{C(Z,S)}{V(Z)}\), or \(\hat{\theta}V(Z) = C(Z,S)\). Then:

\[\begin{align} \hat{\delta} & = \frac{COV(Y,Z)}{COV(S,Z)} \\ & = \frac{\hat{\theta}C(Y,Z)}{\hat{\theta}C(S,Z)} = \frac{\hat{\theta}C(Y,Z)}{\hat{\theta}^{2}V(Z)} \\ & = \frac{C(\hat{\theta}Z,Y)}{V(\hat{\theta}Z)} = \frac{C(\hat{S},Y)}{V(\hat{S})} \end{align}\]

Animation for IV

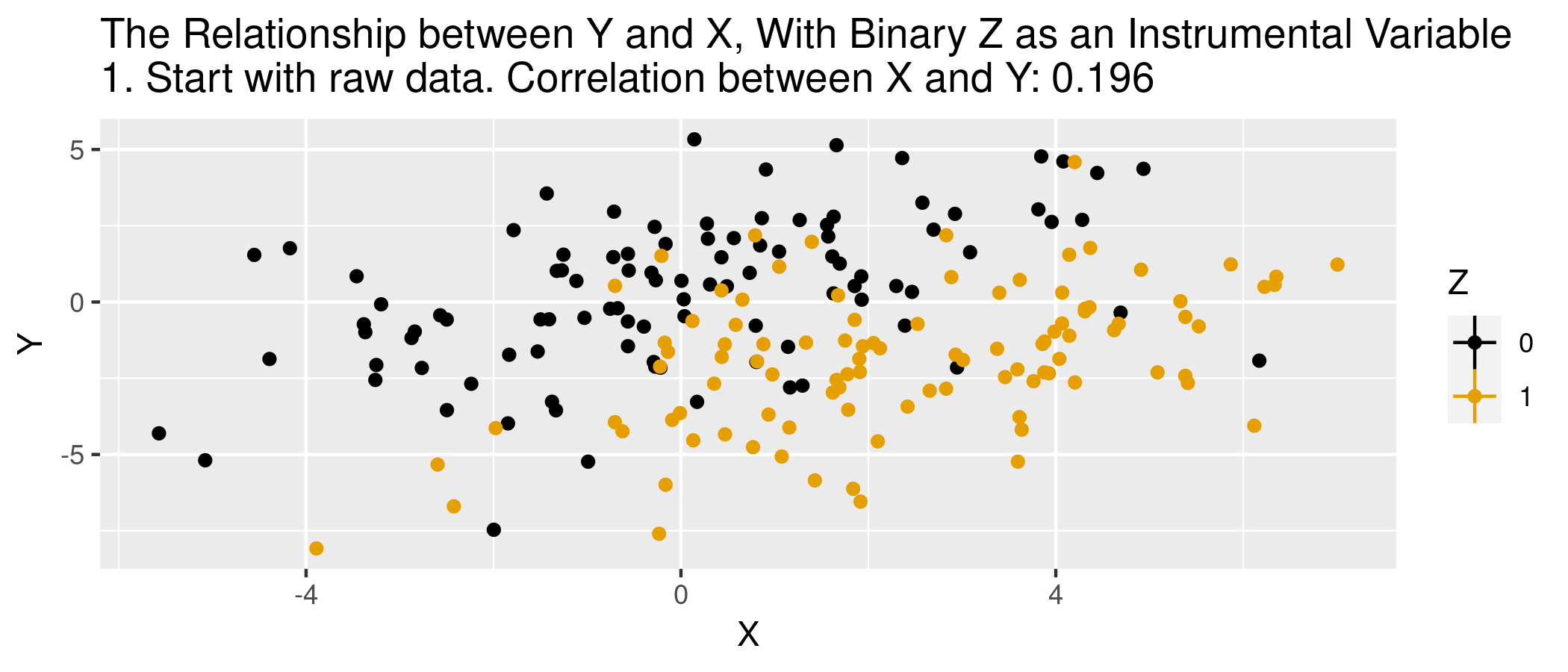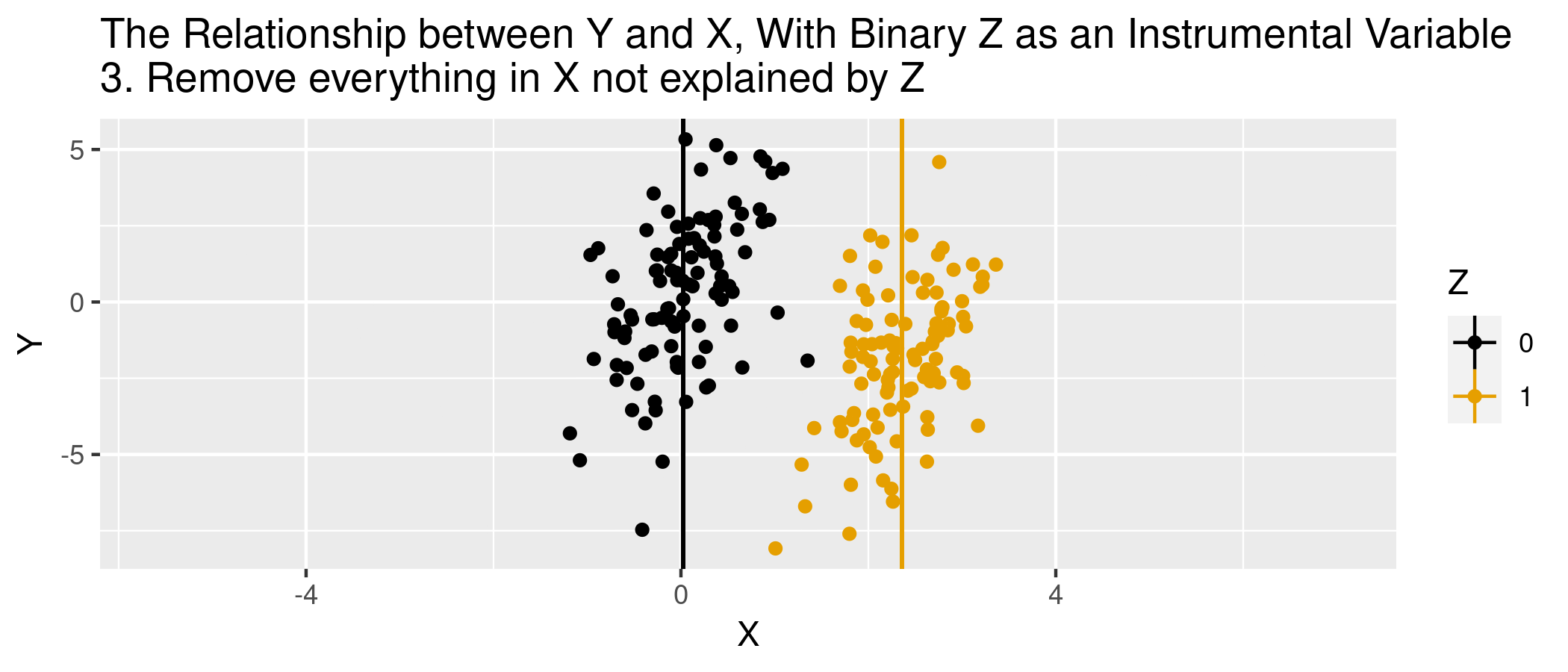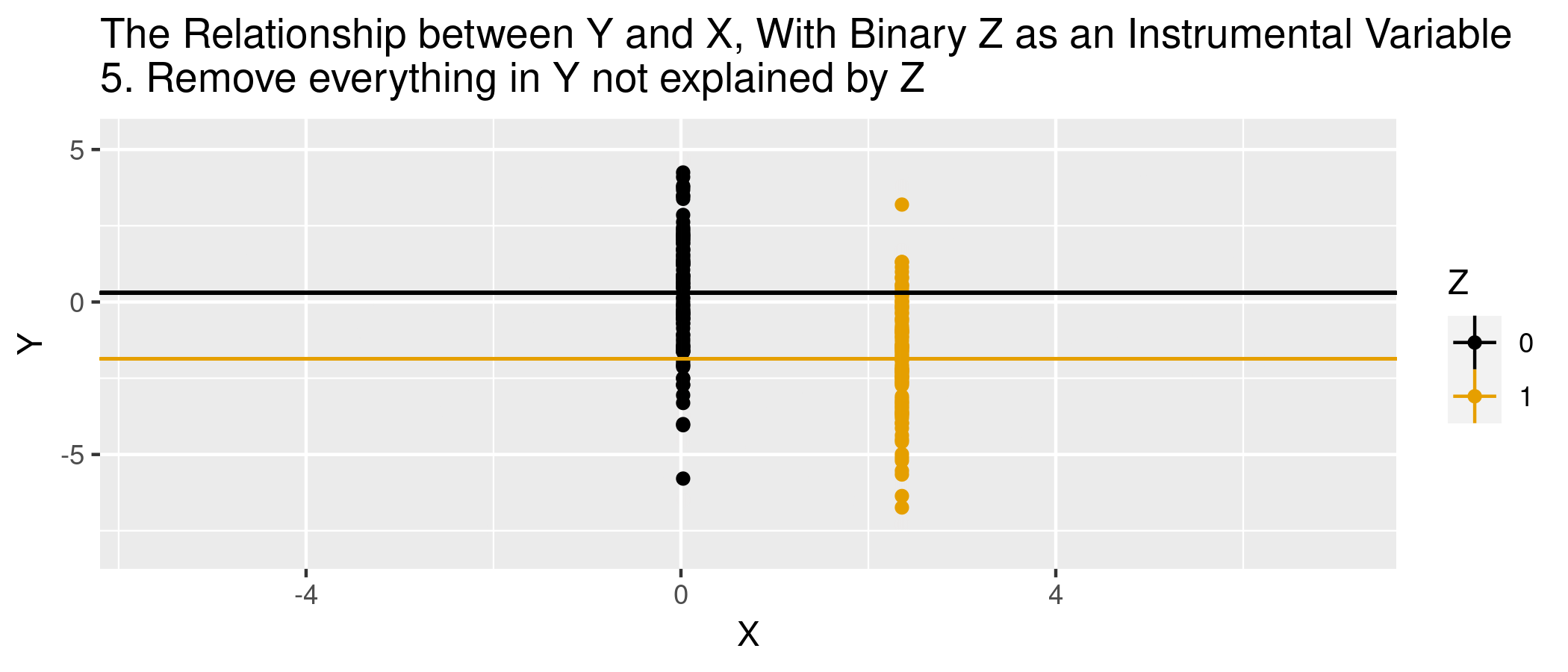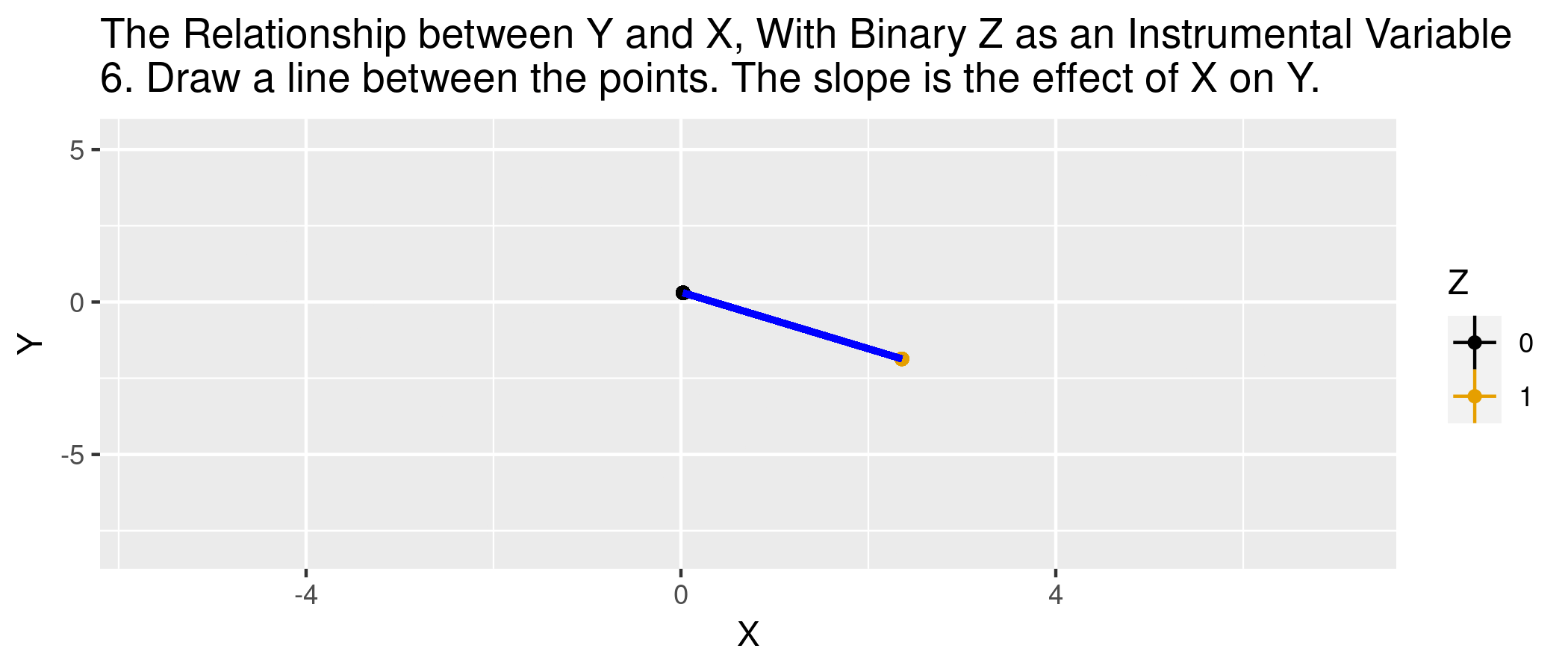
In regression terms

But in practice, DON’T do this in two steps. Why?

Because standard errors are wrong…not accounting for noise in prediction, \(\hat{D}_{i}\). The appropriate fix is built into most modern stats programs.

Formal IV Assumptions

Key assumptions

Exclusion: Instrument is uncorrelated with the error term
Relevance: Instrument is correlated with the endogenous variable
Monotonicity: Treatment more (less) likely for those with higher (lower) values of the instrument

Assumptions 1 and 2 sometimes grouped into an only through condition or discussed as instrument validity

Exclusion Assumption

Not directly testable
Often relies on context and specific policy details

Failure of Exclusion

Conley et al (2010) and “plausible exogeneity”, union of confidence intervals approach

Suppose extent of violation is known in \(y_{i} = \beta x_{i} + \gamma z_{i} + \varepsilon_{i}\), so that \(\gamma = \gamma_{0}\)
IV/TSLS applied to \(y_{i} - \gamma_{0}z_{i} = \beta x_{i} + \varepsilon_{i}\) works
With \(\gamma_{0}\) unknown…do this a bunch of times!
- Pick \(\gamma=\gamma^{b}\) for \(b=1,...,B\)
- Obtain \((1-\alpha)\) % confidence interval for \(\beta\), denoted \(CI^{b}(1-\alpha)\)
- Compute final CI as the union of all \(CI^{b}\)

Failure of Exclusion

Kippersluis and Rietveld (2018), “Beyond Plausibly Exogenous”

“zero-first-stage” test
Focus on subsample for which your instrument is not correlated with the endogenous variable of interest
1. Regress the outcome on all covariates and the instruments among this subsample
2. Coefficient on the instruments captures any potential direct effect of the instruments on the outcome (since the correlation with the endogenous variable is 0 by assumption).

Relevance

Just says that your instrument is correlated with the endogenous variable, but what about the strength of the correlation?

Relevance and Instrument “Strength”

Recall our schooling and wages equation, \[y = \beta S + \epsilon.\] Bias in IV can be represented as:

\[Bias_{IV} \approx \frac{Cov(S, \epsilon)}{V(S)} \frac{1}{F+1} = Bias_{OLS} \frac{1}{F+1}\]

Bias in IV may be close to OLS, depending on instrument strength
Bigger problem: Bias could be bigger than OLS if exclusion restriction not fully satisfied

Testing strength of instruments

Single endogenous variable

Stock & Yogo (2005) test based on first-stage F-stat (homoskedasticity only)
- Critical values in tables, based on number of instruments
- Rule-of-thumb of 10 with single instrument (higher with more instruments)
- Lee et al (2022): With first-stage F-stat of 10, standard “95% confidence interval” for second stage is really an 85% confidence interval
- Over-reliance on “rules of thumb”, as seen in Anders and Kasy (2019)

Testing strength of instruments

Single endogenous variable

Stock & Yogo (2005) test based on first-stage F-stat (homoskedasticity only)
Kleibergen & Paap (2007) Wald statistic
Effective F-statistic from Olea & Pflueger (2013)

Testing strength of instruments: First-stage

Single endogenous variable

Homoskedasticity
- Stock & Yogo, effective F-stat
Heteroskedasticity
- Effective F-stat

Many endogenous variables

Homoskedasticity
- Stock & Yogo with Cragg & Donald statistic, Sanderson & Windmeijer (2016), effective F-stat
Heteroskedasticity
- Kleibergen & Papp Wald is robust analog of Cragg & Donald statistic, effective F-stat

Summary of Instrument Strength

Test first-stage using effective F-stat (inference is harder and beyond this class)
Many endogenous variables problematic because strength of instruments for one variable need not imply strength of instruments for others

IV with Simulated Data

Simulated data

n <- 5000
b.true <- 5.25
iv.dat <- tibble(
  z = rnorm(n,0,2),
  eps = rnorm(n,0,1),
  d = (z + 1.5*eps + rnorm(n,0,1) >0.25),
  y = 2.5 + b.true*d + eps + rnorm(n,0,0.5)
)

endogenous eps: affects treatment and outcome
z is an instrument: affects treatment but no direct effect on outcome

OLS and IV Estimates

Recall that the true treatment effect is 5.25

R
Python
Output

lm(y~d, data=iv.dat)
feols(y ~ 1 | d ~ z, data=iv.dat)

import numpy as np
import pandas as pd

# --- data ---
n = 5000
b_true = 5.25
rng = np.random.default_rng(123)  # for reproducibility

iv_dat = pd.DataFrame({
    "z":   rng.normal(0, 2, n),
    "eps": rng.normal(0, 1, n),
})

iv_dat["d"] = (
    iv_dat["z"] + 1.5 * iv_dat["eps"] + rng.normal(0, 1, n) > 0.25
).astype(int)

iv_dat["y"] = 2.5 + b_true * iv_dat["d"] + iv_dat["eps"] + rng.normal(0, 0.5, n)

# --- OLS: lm(y ~ d) ---
import statsmodels.formula.api as smf

ols = smf.ols("y ~ d", data=iv_dat).fit()
print(ols.summary())

# --- IV/2SLS: feols(y ~ 1 | d ~ z) ---
# (y on intercept, endogenous d, instrument z)
try:
    from linearmodels.iv import IV2SLS

    iv = IV2SLS.from_formula("y ~ 1 + [d ~ z]", data=iv_dat).fit(cov_type="robust")
    print(iv.summary)
except ImportError:
    # Fallback: manual 2SLS using statsmodels
    import statsmodels.api as sm

    first = sm.OLS(iv_dat["d"], sm.add_constant(iv_dat["z"])).fit()
    iv_dat["d_hat"] = first.fittedvalues
    second = sm.OLS(iv_dat["y"], sm.add_constant(iv_dat["d_hat"])).fit()

    print("\nFirst stage (d ~ z):")
    print(first.summary())
    print("\nSecond stage (y ~ d_hat):")
    print(second.summary())


Call:
lm(formula = y ~ d, data = iv.dat)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.5067 -0.6911 -0.0121  0.6953  4.2129 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.10849    0.01956   107.8   <2e-16 ***
dTRUE        6.12514    0.02911   210.4   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.024 on 4998 degrees of freedom
Multiple R-squared:  0.8986,    Adjusted R-squared:  0.8986 
F-statistic: 4.428e+04 on 1 and 4998 DF,  p-value: < 2.2e-16

TSLS estimation - Dep. Var.: y
                  Endo.    : d
                  Instr.   : z
Second stage: Dep. Var.: y
Observations: 5,000
Standard-errors: IID 
            Estimate Std. Error t value  Pr(>|t|)    
(Intercept)   2.5275   0.029102 86.8488 < 2.2e-16 ***
fit_dTRUE     5.1977   0.053966 96.3136 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 1.1233   Adj. R2: 0.877955
F-test (1st stage), dTRUE: stat = 2,691.2, p < 2.2e-16, on 1 and 4,998 DoF.
               Wu-Hausman: stat =   613.7, p < 2.2e-16, on 1 and 4,997 DoF.

Logical Diagnostic: The “Reduced Form”

“Reduced form” means the conditional relationship between the outcome and the instrument (in practice, just replacing the endogenous variable with the instrument in a regression)
While not an official statistical test, empirical researchers often look to the “reduced form” as a reasonableness check of the IV design
- A zero (or wrong-signed) reduced form casts doubt on either relevance or exclusion, but does not tell you which
- A nonzero and properly signed reduced form is necessary for a meaningful IV estimand but provides no validation of exclusion or exogeneity

R
Python
Output

lm(y~z, data=iv.dat)

import statsmodels.formula.api as smf

rf = smf.ols("y ~ z", data=iv_dat).fit()
print(rf.summary())


Call:
lm(formula = y ~ z, data = iv.dat)

Residuals:
   Min     1Q Median     3Q    Max 
-9.164 -2.179 -0.139  2.188  9.412 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  4.88881    0.04001  122.20   <2e-16 ***
z            0.75967    0.01986   38.25   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.829 on 4998 degrees of freedom
Multiple R-squared:  0.2265,    Adjusted R-squared:  0.2263 
F-statistic:  1463 on 1 and 4998 DF,  p-value: < 2.2e-16

lm(d~z, data=iv.dat)

import statsmodels.formula.api as smf

rf = smf.ols("d ~ z", data=iv_dat).fit()
print(rf.summary())


Call:
lm(formula = d ~ z, data = iv.dat)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.14708 -0.32529 -0.02808  0.33542  1.23159 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.454299   0.005676   80.04   <2e-16 ***
z           0.146155   0.002817   51.88   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4013 on 4998 degrees of freedom
Multiple R-squared:   0.35, Adjusted R-squared:  0.3499 
F-statistic:  2691 on 1 and 4998 DF,  p-value: < 2.2e-16

Two-stage equivalence

R
Python
Output

step1 <- lm(d ~ z, data=iv.dat)
d.hat <- predict(step1)
step2 <- lm(y ~ d.hat, data=iv.dat)

import statsmodels.formula.api as smf

# first stage
step1 = smf.ols("d ~ z", data=iv_dat).fit()

# fitted values
iv_dat["d_hat"] = step1.fittedvalues

# second stage
step2 = smf.ols("y ~ d_hat", data=iv_dat).fit()

print(step1.summary())
print(step2.summary())


Call:
lm(formula = y ~ d.hat, data = iv.dat)

Residuals:
   Min     1Q Median     3Q    Max 
-9.164 -2.179 -0.139  2.188  9.412 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.52750    0.07327   34.49   <2e-16 ***
d.hat        5.19770    0.13588   38.25   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.829 on 4998 degrees of freedom
Multiple R-squared:  0.2265,    Adjusted R-squared:  0.2263 
F-statistic:  1463 on 1 and 4998 DF,  p-value: < 2.2e-16

Interpretation

Heterogenous TEs

In constant treatment effects, \(Y_{i}(1) - Y_{i}(0) = \delta_{i} = \delta, \text{ } \forall i\)
Heterogeneous effects, \(\delta_{i} \neq \delta\)
With IV, what parameter did we just estimate? Need monotonicity assumption to answer this

Monotonicity

Assumption: Denote the effect of our instrument on treatment by \(\pi_{1i}\). Monotonicity states that \(\pi_{1i} \geq 0\) or \(\pi_{1i} \leq 0, \text{ } \forall i\).

Allows for \(\pi_{1i}=0\) (no effect on treatment for some people)
All those affected by the instrument are affected in the same “direction”
With heterogeneous ATE and monotonicity assumption, IV provides a “Local Average Treatment Effect” (LATE)

LATE and IV Interpretation

LATE is the effect of treatment among those affected by the instrument (compliers only).
Recall original Wald estimator:

\[\delta_{IV} = \frac{E[Y_{i} | Z_{i}=1] - E[Y_{i} | Z_{i}=0]}{E[D_{i} | Z_{i}=1] - E[D_{i} | Z_{i}=0]}=E[Y_{i}(1) - Y_{i}(0) | \text{complier}]\]

Practically, monotonicity assumes there are no defiers and restricts us to learning only about compliers

Is LATE meaningful?

Learn about average treatment effect for compliers
Different estimates for different compliers
- IV based on merit scholarships
- IV based on financial aid
- Same compliers? Probably not

LATE with defiers

In presence of defiers, IV estimates a weighted difference between effect on compliers and defiers (in general)
LATE can be restored if subgroup of compliers accounts for the same percentage as defiers and has same LATE
Offsetting behavior of compliers and defiers, so that remaining compliers dictate LATE