Difference-in-differences Part I

Ian McCarthy | Emory University

Outline for Today

1. Introduction to Difference-in-Differences
2. Estimators (mean differences and regression)
3. Simulations

Difference-in-Differences

Basic 2x2 Setup

Want to estimate \(ATT = E[Y_{1}(1)- Y_{0}(1) | D=1]\)

	Pre-Period	Post-Period
Treatment	\(E(Y_{0}(0)|D=1)\)	\(E(Y_{1}(1)|D=1)\)
Control	\(E(Y_{0}(0)|D=0)\)	\(E(Y_{0}(1)|D=0)\)

Problem: We don’t see \(E[Y_{0}(1)|D=1]\)

Basic 2x2 Setup

Want to estimate \(ATT = E[Y_{1}(1)- Y_{0}(1) | D=1]\)

	Pre-Period	Post-Period
Treatment	\(E(Y_{0}(0)|D=1)\)	\(E(Y_{1}(1)|D=1)\)
Control	\(E(Y_{0}(0)|D=0)\)	\(E(Y_{0}(1)|D=0)\)

Strategy 1: Estimate \(E[Y_{0}(1)|D=1]\) using \(E[Y_{0}(0)|D=1]\) (before treatment outcome used to estimate post-treatment)

Strategy 2: Estimate \(E[Y_{0}(1)|D=1]\) using \(E[Y_{0}(1)|D=0]\) (control group used to predict outcome for treatment)

Strategy 3: Estimate \(E[Y_{1}(1)|D=1] - E[Y_{0}(1)|D=1]\) using \(E[Y_{0}(1)|D=0] - E[Y_{0}(0)|D=0]\) (pre-post difference in control group used to predict difference for treatment group). This is DD!

Graphically

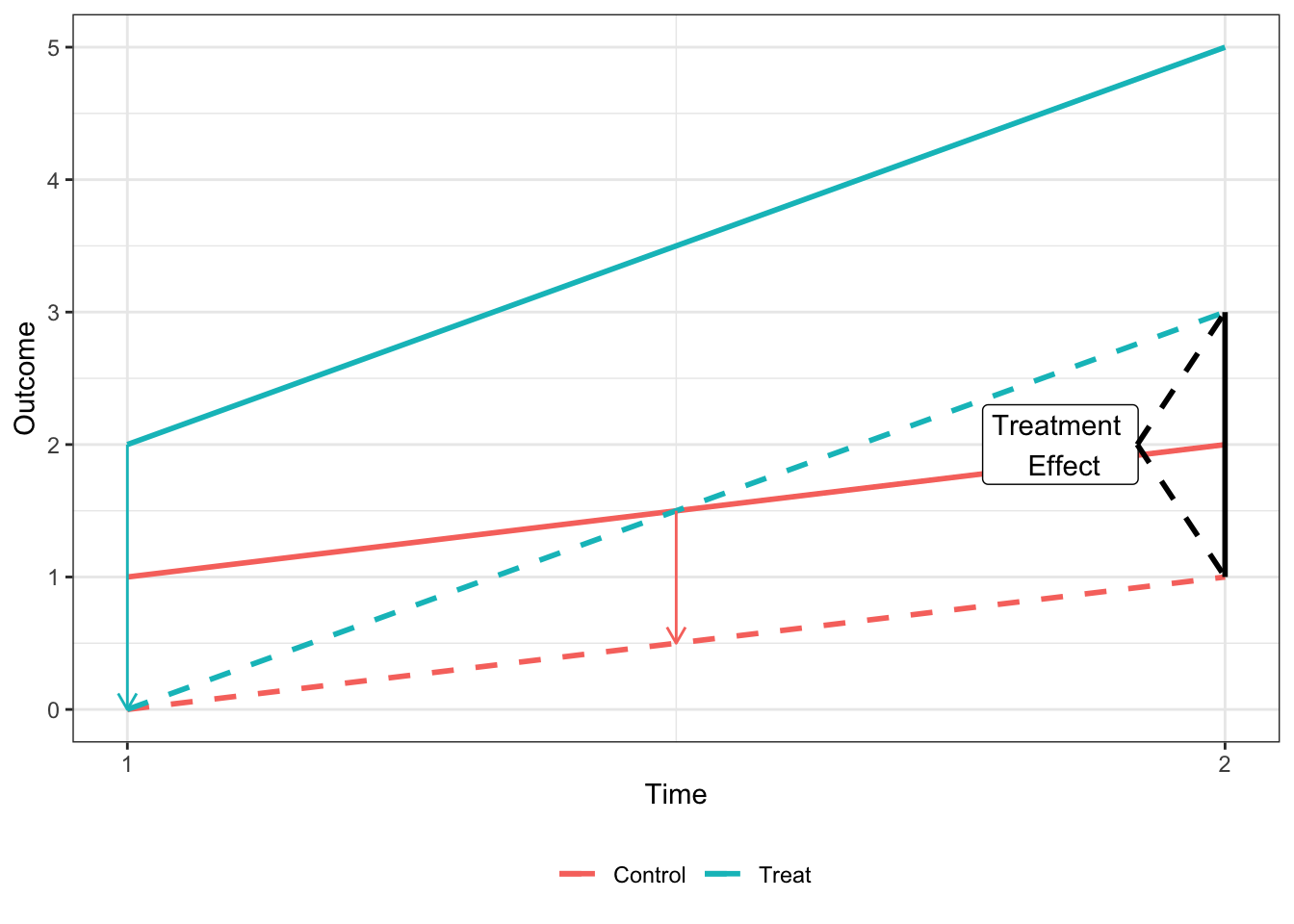
Basic DD Graph

Animations

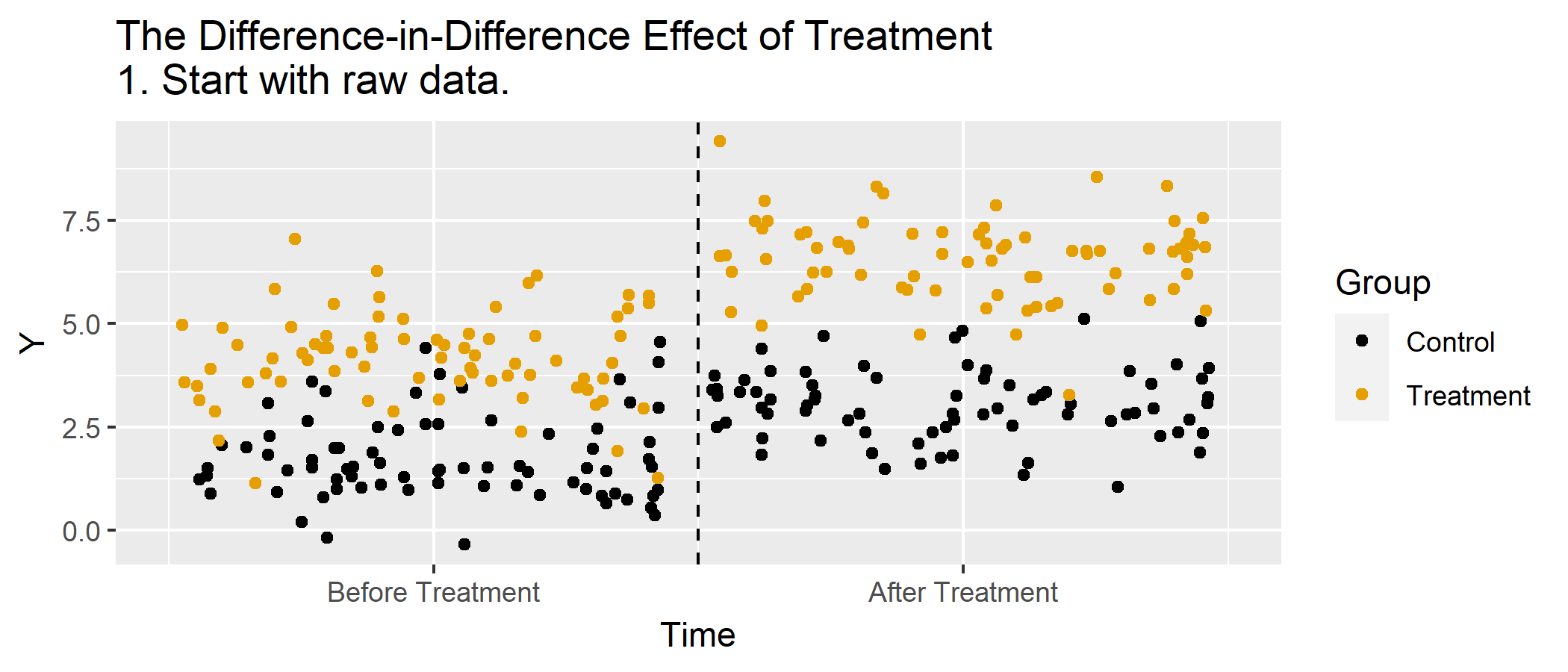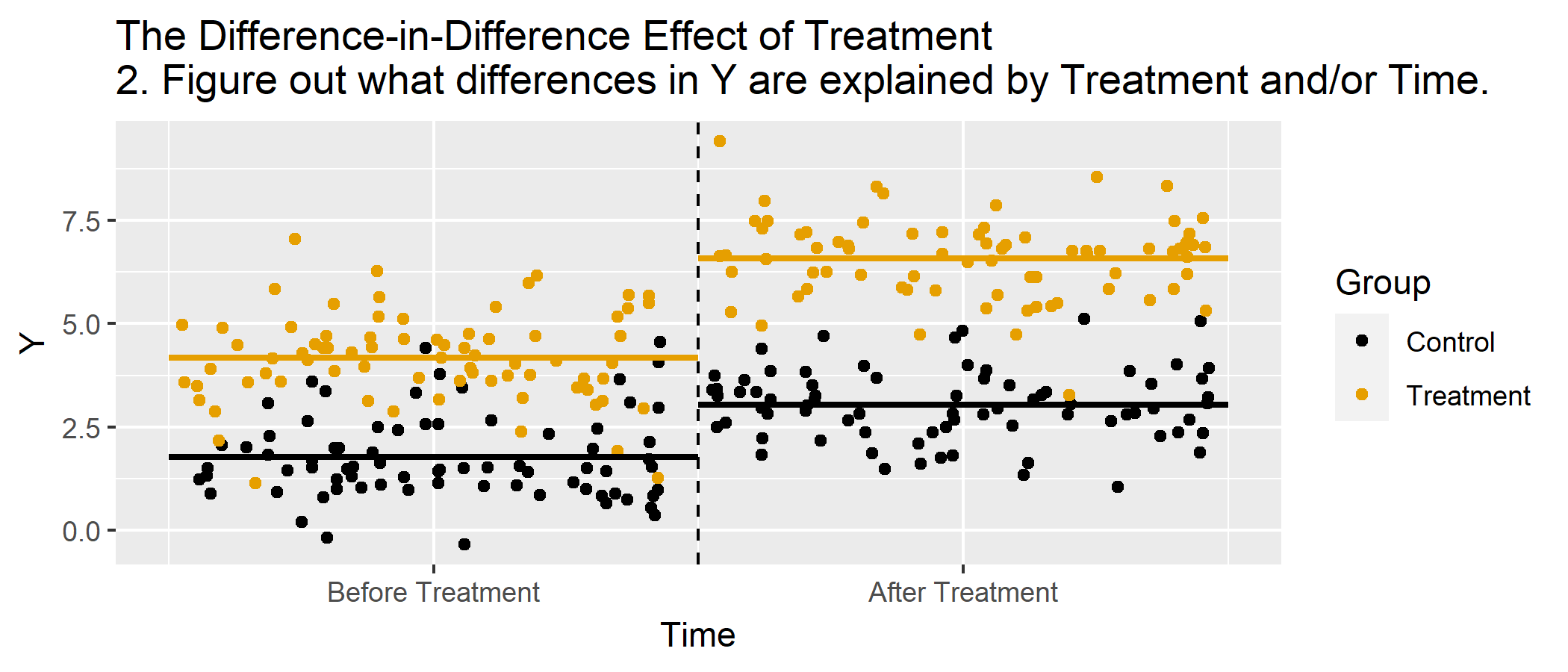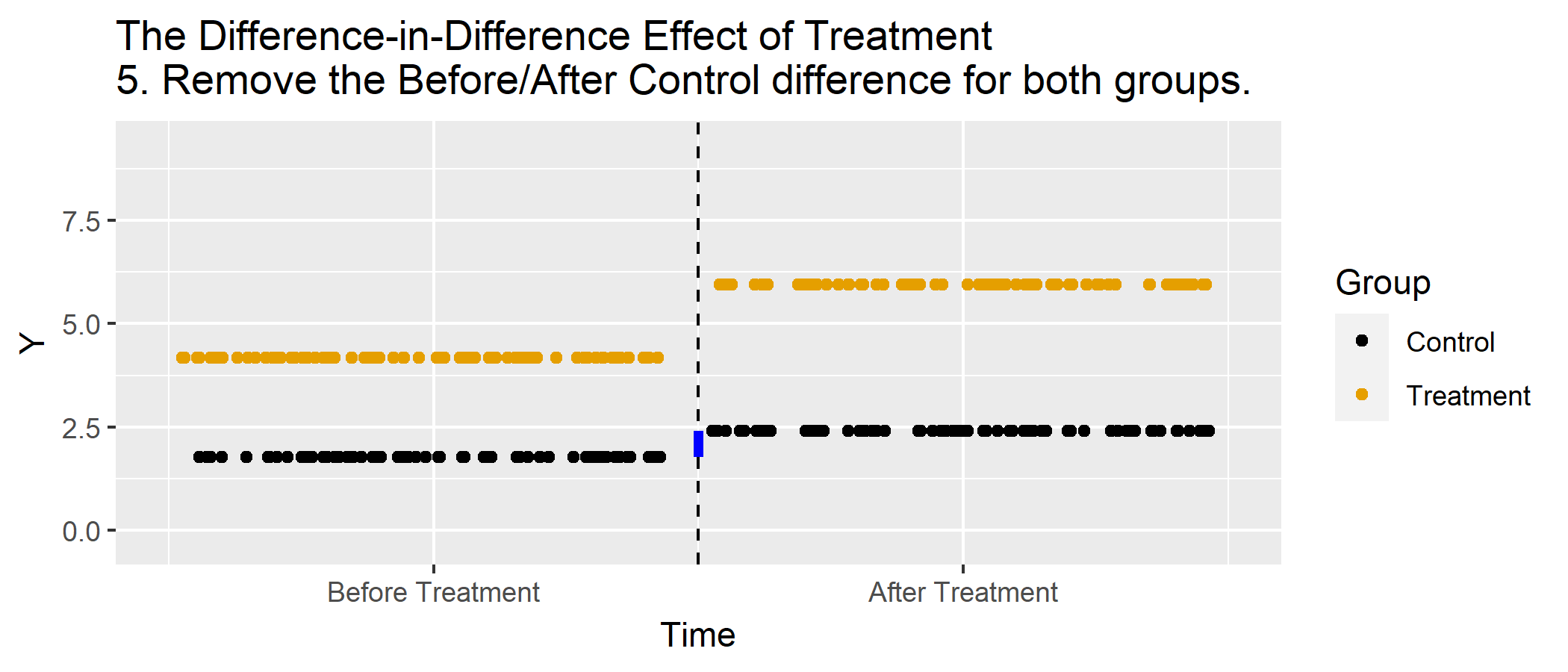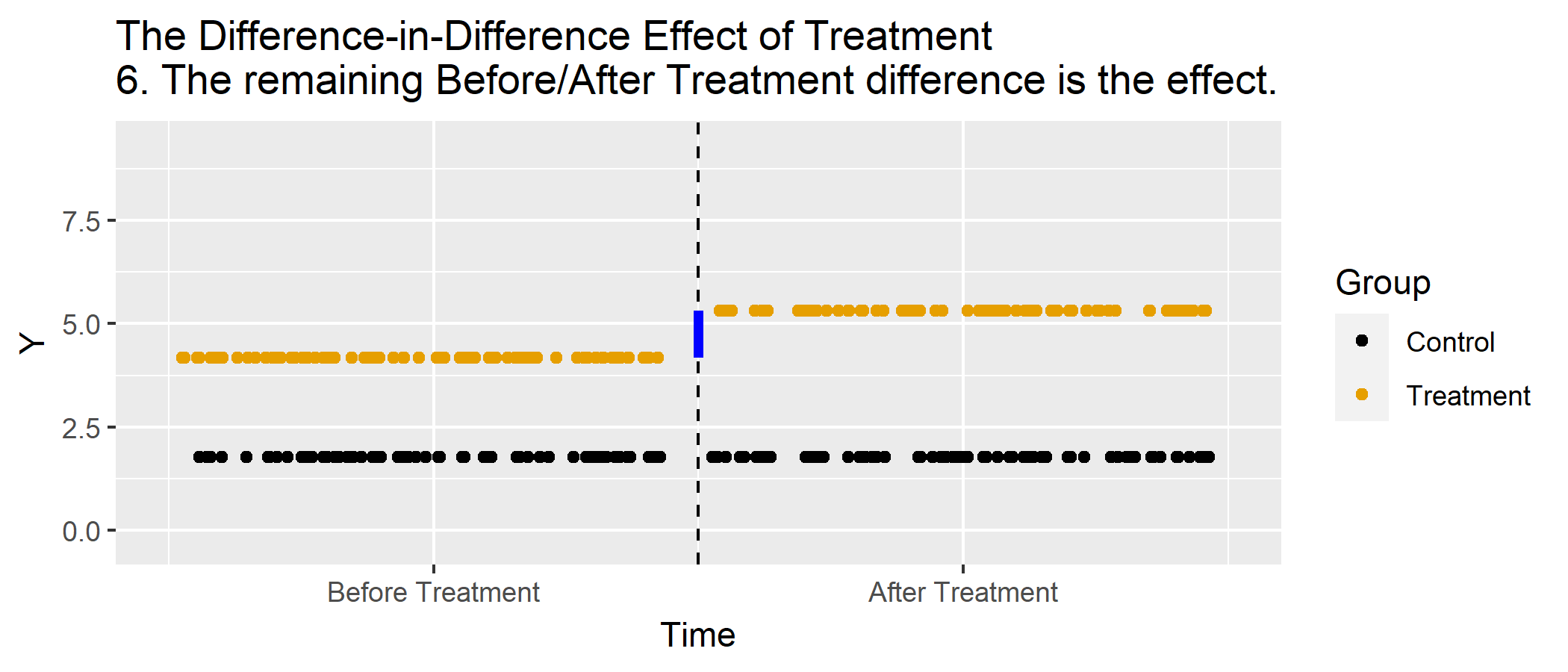
Basic DD Graph, Animated

DD “Estimators”

Key Assumption

Key identifying assumption is that of parallel trends

\[E[Y_{0}(1) - Y_{0}(0)|D=1] = E[Y_{0}(1) - Y_{0}(0)|D=0]\]

Estimation: Sample Means

\[\begin{align} E[Y_{1}(1) - Y_{0}(1)|D=1] &=& \left( E[Y(1)|D=1] - E[Y(1)|D=0] \right) \\ & & - \left( E[Y(0)|D=1] - E[Y(0)|D=0]\right) \end{align}\]

Estimation: Regression

\[y_{it} = \alpha + \beta D_{i} + \lambda \times Post_{t} + \delta \times D_{i} \times Post_{t} + \varepsilon_{it}\]

	Pre	Post	Post - Pre
Treatment	\(\alpha + \beta\)	\(\alpha + \beta + \lambda + \delta\)	\(\lambda + \delta\)
Control	\(\alpha\)	\(\alpha + \lambda\)	\(\lambda\)
Diff	\(\beta\)	\(\beta + \delta\)	\(\delta\)

Simulations

The data

• R
• Python
• Output

set.seed(123)
N <- 5000

dd.dat <- tibble(
  d = (runif(N, 0, 1) > 0.5),
  time_pre = "pre",
  time_post = "post"
)

dd.dat <- pivot_longer(dd.dat, c("time_pre", "time_post"), values_to = "time") %>%
  select(d, time) %>%
  mutate(
    t = (time == "post"),
    y.out = 1.5 + 3 * d + 1.5 * t + 6 * d * t + rnorm(N * 2, 0, 1)
  )

import numpy as np
import pandas as pd

rng = np.random.default_rng(123)
N = 5000

base = pd.DataFrame({
    "d": rng.uniform(0, 1, N) > 0.5,
    "time_pre": "pre",
    "time_post": "post"
})

dd_dat = (
    base
    .melt(value_vars=["time_pre", "time_post"], value_name="time")
    .loc[:, ["d", "time"]]
)

dd_dat["t"] = dd_dat["time"] == "post"

dd_dat["y_out"] = (
    1.5
    + 3 * dd_dat["d"].astype(int)
    + 1.5 * dd_dat["t"].astype(int)
    + 6 * dd_dat["d"].astype(int) * dd_dat["t"].astype(int)
    + rng.normal(0, 1, N * 2)
)

# A tibble: 6 × 4
  d     time  t      y.out
  <lgl> <chr> <lgl>  <dbl>
1 FALSE pre   FALSE  0.821
2 FALSE post  TRUE   3.57 
3 TRUE  pre   FALSE  3.80 
4 TRUE  post  TRUE  11.5  
5 FALSE pre   FALSE  2.27 
6 FALSE post  TRUE   2.52 

Mean differences

• R
• Python
• Output

dd.means <- dd.dat %>%
  group_by(d, t) %>%
  summarize(mean_y = mean(y.out), .groups = "drop") %>%
  mutate(
    d = ifelse(d == TRUE, "Treated", "Control"),
    t = ifelse(t == TRUE, "Post", "Pre")
  )

import pandas as pd

dd_means = (
    dd_dat
    .groupby(["d", "t"], as_index=False)
    .agg(mean_y=("y_out", "mean"))
)

dd_means["d"] = dd_means["d"].map({True: "Treated", False: "Control"})
dd_means["t"] = dd_means["t"].map({True: "Post", False: "Pre"})

print(dd_means)

Treated	Period	Mean
Control	Pre	1.519301
Control	Post	2.963925
Treated	Pre	4.482393
Treated	Post	12.019518

Mean differences

In this example:

• \(E[Y(1)|D=1] - E[Y(1)|D=0]\) is 9.0555937
• \(E[Y(0)|D=1] - E[Y(0)|D=0]\) is 2.9630918

So the ATT is 6.092502

Regression estimator

• R
• Python
• Output

library(modelsummary)
dd.est <- lm(y.out ~ d + t + d * t, data = dd.dat)

import statsmodels.formula.api as smf

dd_dat_for_reg = dd_dat.copy()

dd_dat_for_reg["d"] = dd_dat_for_reg["d"].astype(int)
dd_dat_for_reg["t"] = dd_dat_for_reg["t"].astype(int)

dd_est = smf.ols("y_out ~ d + t + d:t", data=dd_dat_for_reg).fit()
print(dd_est.summary())

	(1)
dTRUE	2.963
	(0.028)
tTRUE	1.445
	(0.028)
dTRUE × tTRUE	6.093
	(0.040)