hcris.data <- read_csv("../data/output/hcris-snippets/hcris-data.csv") %>%
mutate(
expand_year = lubridate::year(date_adopted),
expand_ever = expanded,
status = if_else(!is.na(expand_year) & year >= expand_year, "Expanded", "Not Expanded"),
uncomp_care_m = uncomp_care / 1e6
) %>%
filter(!is.na(expand_ever))
uc.plot.dat <- hcris.data %>%
group_by(expand_ever, year) %>%
summarize(mean = mean(uncomp_care_m, na.rm = TRUE), .groups = "drop")
uc.plot <- ggplot(data = uc.plot.dat, aes(x = year, y = mean, group = expand_ever, linetype = expand_ever)) +
geom_line() + geom_point() + theme_bw() +
geom_vline(xintercept = 2013.5, color = "red") +
geom_text(data = uc.plot.dat %>% filter(year == 2015),
aes(label = c("Non-expansion", "Expansion"),
x = year + 1,
y = mean)) +
guides(linetype = "none") +
labs(
x = "Year",
y = "Uncompensated Care ($mm)",
title = "Hospital Uncompensated Care Over Time"
)Difference-in-differences Part II
Outline for Today
- Simple DD
- TWFE
- Event Studies
- “Modern” Considerations
Simple DD in Practice
- Try out some real data on Medicaid expansion following the ACA
- Data is small part of DD empirical assignment
- Question: Did Medicaid expansion reduce hospital uncompensated care?
Step 1: Look at the data
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
hcris_data = pd.read_csv("../data/output/hcris-snippets/hcris-data.csv")
hcris_data["expand_year"] = pd.to_datetime(hcris_data["date_adopted"]).dt.year
hcris_data["expand_ever"] = hcris_data["expanded"]
hcris_data["status"] = np.where(
(~hcris_data["expand_year"].isna()) & (hcris_data["year"] >= hcris_data["expand_year"]),
"Expanded",
"Not Expanded"
)
hcris_data["uncomp_care_m"] = hcris_data["uncomp_care"] / 1_000_000
hcris_data = hcris_data.loc[~hcris_data["expand_ever"].isna()].copy()
uc_plot_dat = (
hcris_data
.groupby(["expand_ever", "year"], as_index=False)
.agg(mean=("uncomp_care_m", "mean"))
)
# Example plot in Python (kept minimal since output is shown from R)
for key, grp in uc_plot_dat.groupby("expand_ever"):
plt.plot(grp["year"], grp["mean"], marker="o", label=str(key))
plt.axvline(2013.5, color="red")
plt.xlabel("Year")
plt.ylabel("Uncompensated Care ($mm)")
plt.title("Hospital Uncompensated Care Over Time")
plt.legend()
plt.show()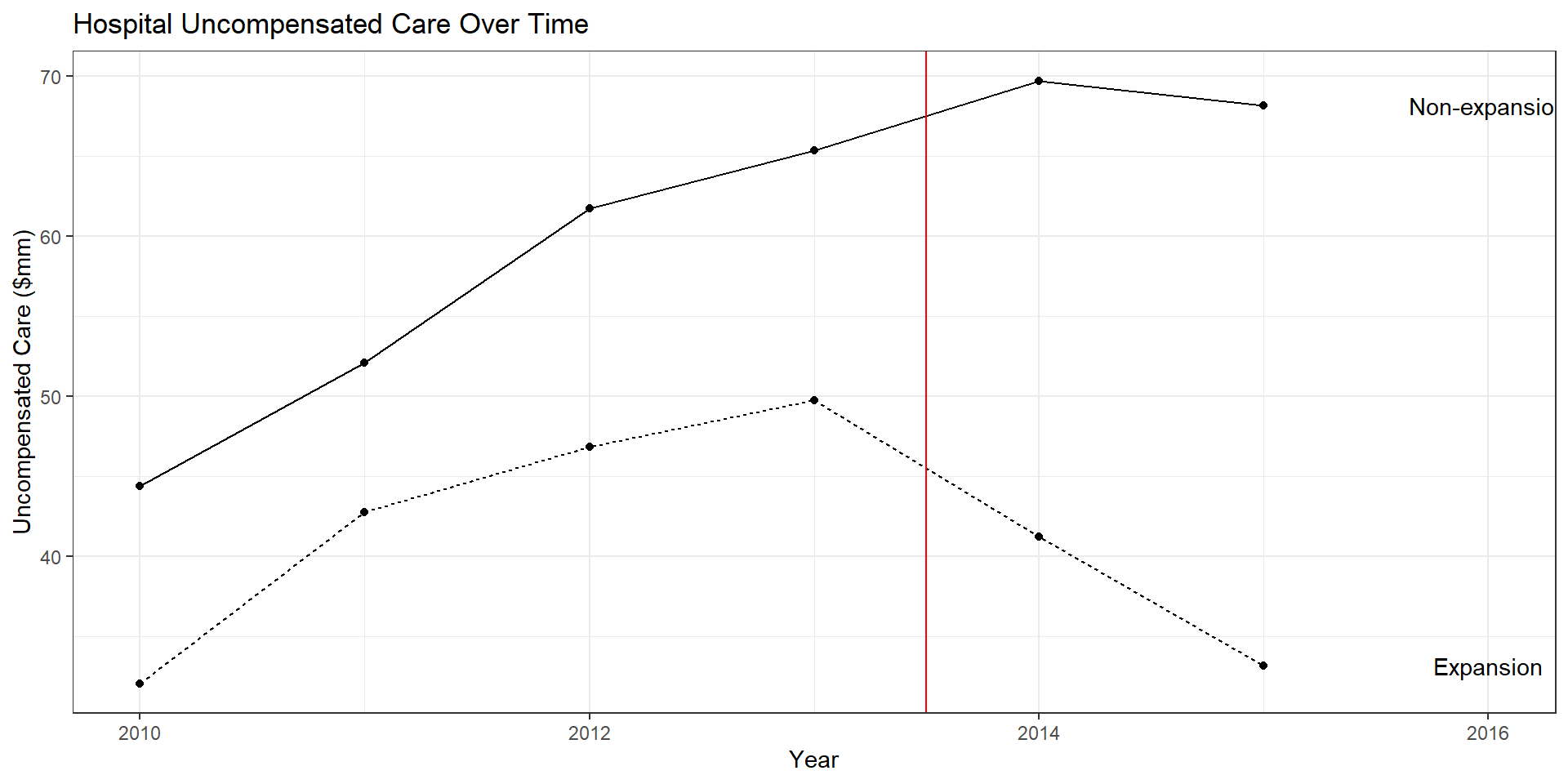
Step 2: Estimate effects
Interested in \(\delta\) from:
\[y_{it} = \alpha + \beta \times Post_{t} + \lambda \times Expand_{i} + \delta \times Post_{t} \times Expand_{i} + \varepsilon_{it}\]
import statsmodels.formula.api as smf
reg_dat = hcris_data.loc[
(hcris_data["expand_year"].eq(2014)) | (hcris_data["expand_year"].isna())
].copy()
reg_dat["post"] = reg_dat["year"] >= 2014
reg_dat["treat"] = reg_dat["post"] & reg_dat["expand_ever"]
reg_dat["post"] = reg_dat["post"].astype(int)
reg_dat["expand_ever"] = reg_dat["expand_ever"].astype(int)
reg_dat["treat"] = reg_dat["treat"].astype(int)
reg_dat["uncomp_care_m"] = reg_dat["uncomp_care"] / 1_000_000
dd_uc_reg = smf.ols("uncomp_care_m ~ post + expand_ever + post:expand_ever", data=reg_dat).fit()
print(dd_uc_reg.summary())| DD (2014) | |
|---|---|
| postTRUE | 13.620 |
| (3.434) | |
| expand_everTRUE | -11.665 |
| (8.710) | |
| postTRUE × expand_everTRUE | -22.047 |
| (4.118) |
Final DD thoughts
- Key identification assumption is parallel trends
- Inference: Typically want to cluster at unit-level to allow for correlation over time within units, but problems with small numbers of treated or control groups:
- Conley-Taber CIs
- Wild cluster bootstrap
- Randomization inference
- “Extra” things like propensity score weighting and doubly robust estimation
Two-way fixed effects (TWFE)
DD and TWFE?
- Just a shorthand for a common regression specification
- Fixed effects for each unit and each time period, \(\gamma_{i}\) and \(\gamma_{t}\)
- More general than 2x2 DD but same result
What is TWFE?
Want to estimate \(\delta\):
\[y_{it} = \alpha + \delta D_{it} + \gamma_{i} + \gamma_{t} + \varepsilon_{it},\]
where \(\gamma_{i}\) and \(\gamma_{t}\) denote a set of unit \(i\) and time period \(t\) dummy variables (or fixed effects).
TWFE in Practice
import statsmodels.formula.api as smf
# 2x2 DD (OLS)
m_dd = smf.ols("uncomp_care_m ~ post + expand_ever + treat", data=reg_dat).fit()
# TWFE using unit and year dummies
m_twfe = smf.ols("uncomp_care_m ~ treat + C(provider_number) + C(year)", data=reg_dat).fit()
print(m_dd.summary())
print(m_twfe.summary())| DD | TWFE | |
|---|---|---|
| postTRUE | 13.620 | |
| (3.434) | ||
| expand_everTRUE | -11.665 | |
| (8.710) | ||
| treat | -22.047 | -23.217 |
| (4.118) | (4.548) |
Event Studies
Basic idea
Event study is poorly named:
- In finance, even study is just an interrupted time series
- In econ and other areas, we usually have a treatment/control group and a break in time
Why show an event study?
- Allows for heterogeneous effects over time (maybe effects phase in over time or dissipate)
- Visually very appealing
- Offers easy evidence against or consistent with parallel trends assumption
How to do an event study?
Estimate something akin to… \[y_{it} = \gamma_{i} + \gamma_{t} + \sum_{\tau = -q}^{-2}\delta_{\tau} D_{i \tau} + \sum_{\tau=0}^{m} \delta_{\tau}D_{i \tau} + \beta x_{it} + \epsilon_{it},\]
where \(q\) captures the number of periods before the treatment occurs and \(m\) captures periods after treatment occurs.
How to do an event study?
- Create all treatment/year interactions
- Regressions with full set of interactions and group/year FEs
- Plot coefficients and standard errors
Things to address
- “Event time” vs calendar time
- Define baseline period
- Choose number of pre-treatment and post-treatment coefficients
Event time vs calendar time
Essentially two “flavors” of event studies
- Common treatment timing
- Differential treatment timing
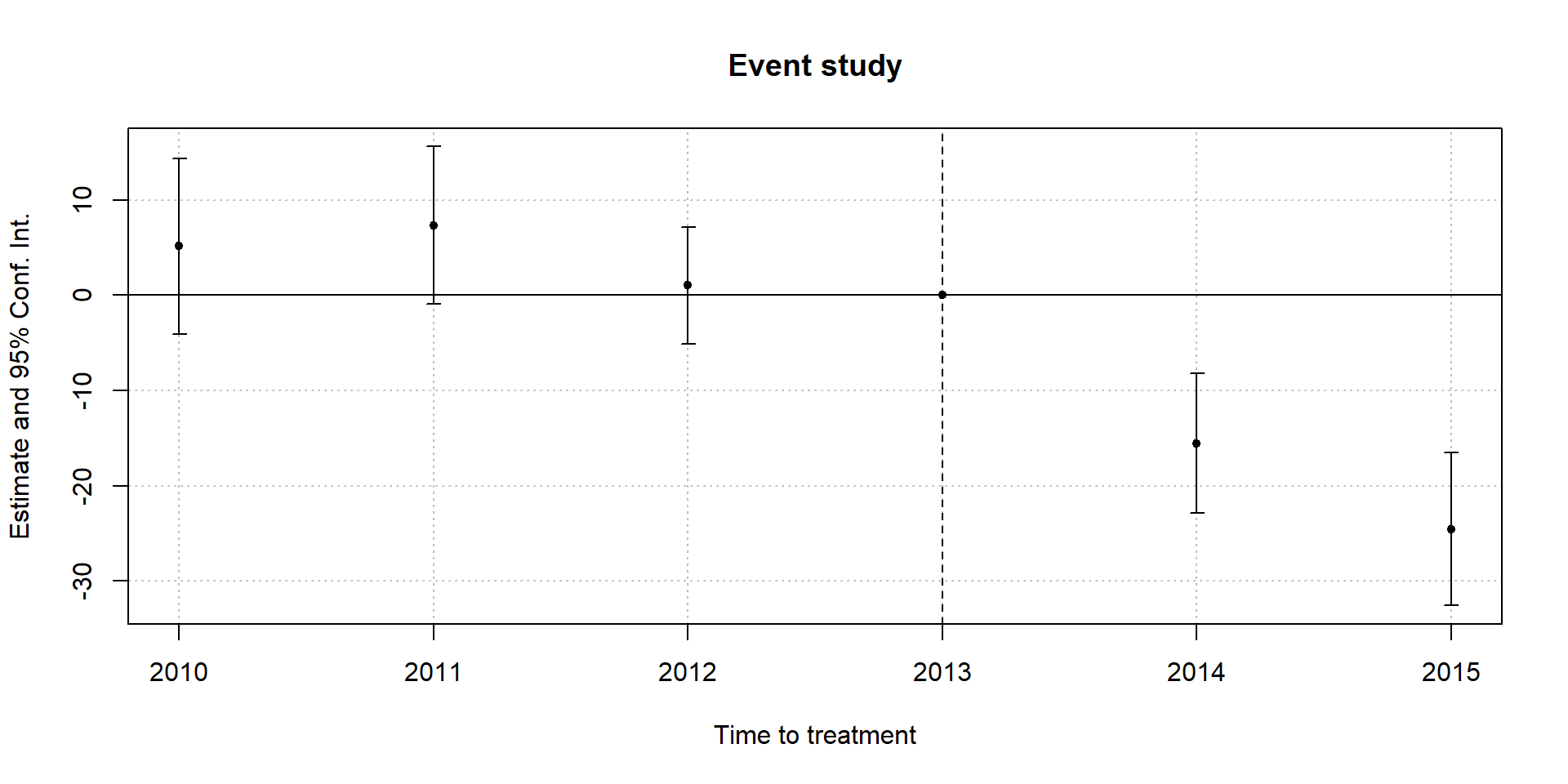
Define baseline period
- Must choose an “excluded” time period (as in all cases of group dummy variables)
- Common choice is \(t=-1\) (period just before treatment)
- Easy to understand with calendar time
- For event time…manually set time to \(t=-1\) for all untreated units
Number of pre-treatment and post-treatment periods
- On event time, sometimes very few observations for large lead or lag values
- Medicaid expansion example: Late adopting states have fewer post-treatment periods
- Norm is to group final lead/lag periods together
Common treatment timing
Differential treatment timing
- Now let’s work with the full Medicaid expansion data
- Includes late adopters
- Requires putting observations on “event time”
Differential treatment timing
reg.dat.full <- hcris.data %>%
filter(!is.na(expand_ever)) %>%
mutate(
time_to_treat = if_else(expand_ever == FALSE, 0, year - expand_year),
time_to_treat = if_else(time_to_treat < -3, -3, time_to_treat)
)
mod.twfe.full <- feols(uncomp_care_m ~ i(time_to_treat, expand_ever, ref = -1) | provider_number + year,
cluster = ~ state,
data = reg.dat.full)reg_dat_full = hcris_data.loc[~hcris_data["expand_ever"].isna()].copy()
reg_dat_full["time_to_treat"] = np.where(
reg_dat_full["expand_ever"].astype(bool),
reg_dat_full["year"] - reg_dat_full["expand_year"],
0
)
reg_dat_full["time_to_treat"] = reg_dat_full["time_to_treat"].clip(lower=-3)
mod_twfe_full = smf.ols(
"uncomp_care_m ~ C(time_to_treat)*expand_ever + C(provider_number) + C(year)",
data=reg_dat_full
).fit()
print(mod_twfe_full.summary())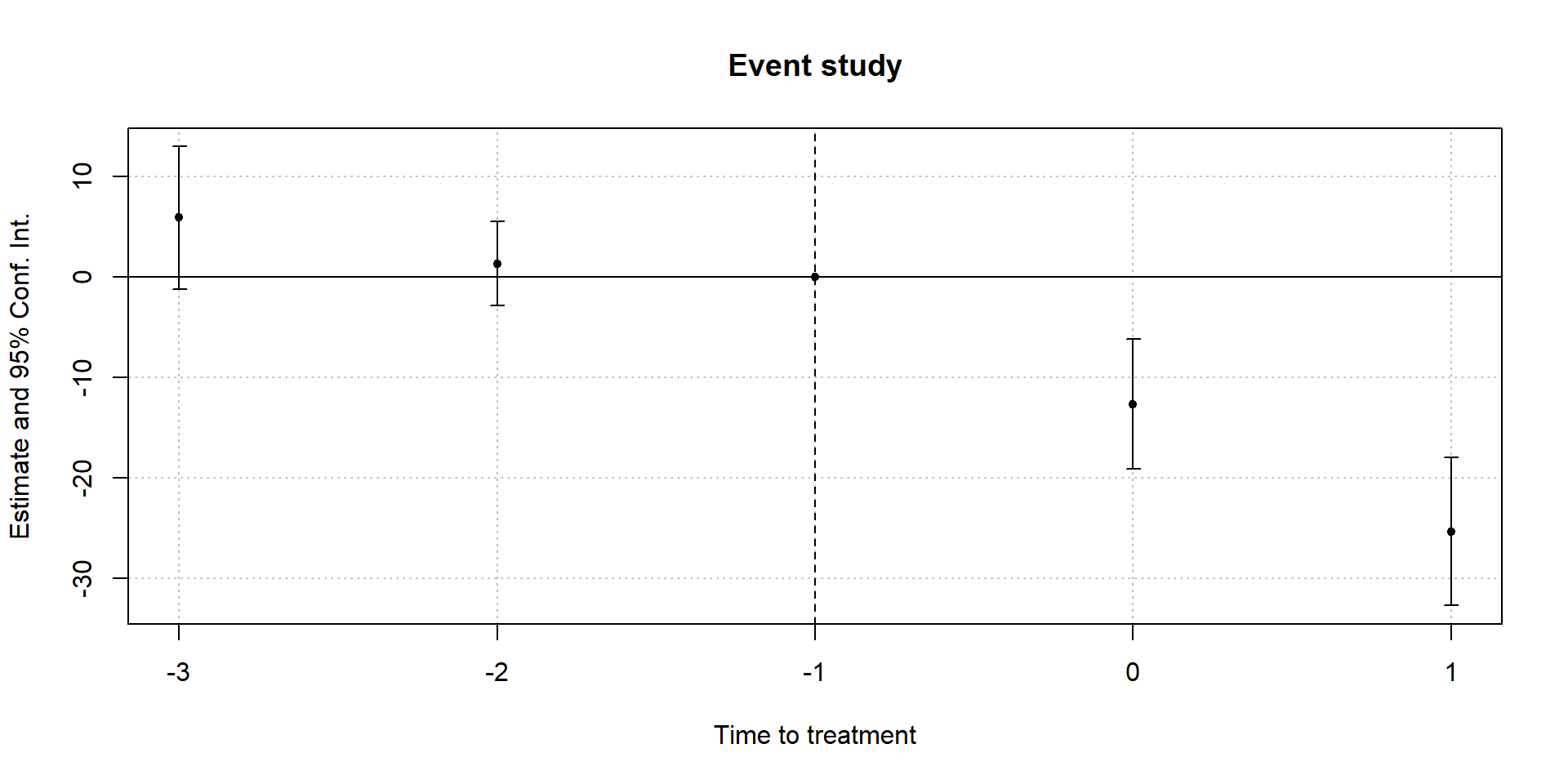
“Modern” Considerations
Problems with TWFE
- Recall goal of estimating ATE or ATT
- TWFE and 2x2 DD identical with homogeneous effects and common treatment timing
- Otherwise…TWFE is biased and inconsistent for ATT
Consider standard TWFE specification with a single treatment coefficient, \[y_{it} = \alpha + \delta D_{it} + \gamma_{i} + \gamma_{t} + \varepsilon_{it}.\] We can decompose \(\hat{\delta}\) into three things:
\[\hat{\delta}_{twfe} = \text{VW} ATT + \text{VW} PT - \Delta ATT\]
- A variance-weighted ATT
- Violation of parallel trends
- Heterogeneous effects over time
Intuition
Problems come from heterogeneous effects and staggered treatment timing
- OLS is a weighted average of all 2x2 DD groups
- Weights are function of size of subsamples, size of treatment/control units, and timing of treatment
- Units treated in middle of sample receive larger weights
- Best case: Variance-weighted ATT
- Prior-treated units act as controls for late-treated units, so differential timing alone can introduce bias
- Heterogeneity and differential timing introduces “contamination” via negative weights assigned to some underlying 2x2 DDs
Does it really matter?
- Definitely! But how much?
- Large treatment effects for early treated units could reverse the sign of final estimate
- Several “modern” approaches to address these issues
New DD: Callaway & Sant’Anna (Group-Time ATT)
- Estimates group-by-time ATT, then aggregates into overall effects
- Handles staggered adoption with flexible aggregation and clear identification targets
- Separates identification from weighting choices explicitly
New DD: Sun & Abraham (Interaction-Weighted Event Study)
- Corrects TWFE event-study bias under staggered adoption
- Uses cohort-by-time interactions and aggregates appropriately
- Clean interpretation for dynamic effects relative to treatment timing
New DD: Borusyak, Jaravel, Spiess (Imputation Estimator)
- Imputes untreated potential outcomes using pre-treatment trends
- Estimates treatment effects by comparing observed outcomes to imputed counterfactuals
- Transparent decomposition and robust to staggered timing
New DD: Gardner (Two-Stage DID)
- Stage 1 removes unit and time effects using untreated data
- Stage 2 estimates treatment effects on residualized outcomes
- Useful when treatment timing is staggered and effects are heterogeneous