Introduction to Causal Inference

Ian McCarthy | Emory University

Why causal inference?

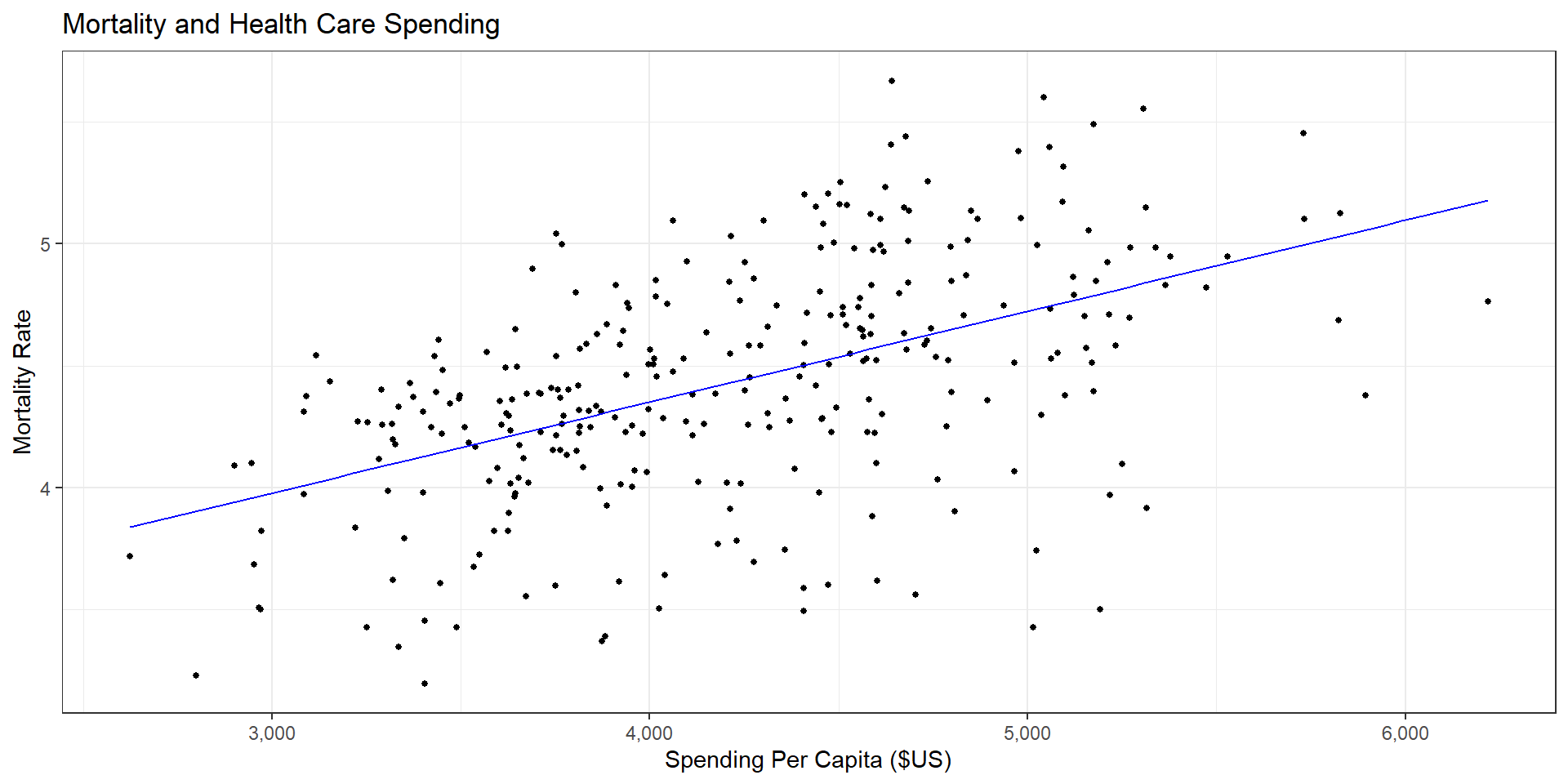
R Code

ggplot(data = (dartmouth.data %>% filter(Year==2015)), 
       mapping = aes(x = Expenditures, y = Total_Mortality)) + 
  geom_point(size = 1) + theme_bw() + scale_x_continuous(label = comma) +
  geom_smooth(method="lm", se=FALSE, color="blue", size=1/2) +
  labs(x = "Spending Per Capita ($US)",
       y = "Mortality Rate",
       title = "Mortality and Health Care Spending")

Why causal inference?

Another example: What price should we charge for a night in a hotel?

Machine Learning

• Focuses on prediction
• High prices are strongly correlated with higher sales
• Increase prices to attract more people?

Causal Inference

• Focuses on counterfactuals
• What would sales look like if prices were higher?

Goal of Causal Inference

• Goal: Estimate effect of some policy or program
• Key building block for causal inference is the idea of potential outcomes

Some notation

Treatment \(D_{i}\)

\[D_{i}=\begin{cases} 1 \text{ with treatment} \\ 0 \text{ without treatment} \end{cases}\]

Some notation

Potential outcomes

• \(Y_{1i}\) is the potential outcome for unit \(i\) with treatment
• \(Y_{0i}\) is the potential outcome for unit \(i\) without treatment

Some notation

Observed outcome

\[Y_{i}=Y_{1i} \times D_{i} + Y_{0i} \times (1-D_{i})\] or

\[Y_{i}=\begin{cases} Y_{1i} \text{ if } D_{i}=1 \\ Y_{0i} \text{ if } D_{i}=0 \end{cases}\]

Assumes SUTVA (stable unit treatment value assumption)…no interference across units

Example of “Potential Outcomes”

\(Y_{1}\)= $75,000

\(Y_{0}\)= $60,000

Single-year earnings due to Emory = \(Y_{1}-Y_{0}\) = $15,000

Example of “Potential Outcomes”

\(Y_{1}\)= $75,000

\(Y_{0}\)= ?

Earnings due to Emory = \(Y_{1}-Y_{0}\) = ?

Do we ever observe the potential outcomes?

Without a time machine…not possible to get individual effects.

Fundamental Problem of Causal Inference

• We don’t observe the counterfactual outcome…what would have happened if a treated unit was actually untreated.
• ALL attempts at causal inference represent some attempt at estimating the counterfactual outcome. We need an estimate for \(Y_{0}\) among those that were treated, and vice versa for \(Y_{1}\).

Average Treatment Effects

Different treatment effects

Tend to focus on averages:

• ATE: \(\delta_{ATE} = E[ Y_{1} - Y_{0}]\)
• ATT: \(\delta_{ATT} = E[ Y_{1} - Y_{0} | D=1]\)
• ATU: \(\delta_{ATU} = E[ Y_{1} - Y_{0} | D=0]\)

or similar measures such as medians or quantiles

Average Treatment Effects

• Estimand: \[\delta_{ATE} = E[Y_{1} - Y_{0}] = E[Y | D=1] - E[Y | D=0]\]
• Estimate: \[\hat{\delta}_{ATE} = \frac{1}{N_{1}} \sum_{D_{i}=1} Y_{i} - \frac{1}{N_{0}} \sum_{D_{i}=0} Y_{i},\] where \(N_{1}\) is number of treated and \(N_{0}\) is number untreated (control)
• With random assignment and equal groups, inference/hypothesis testing with standard two-sample t-test

Problem of non-random assignment

Selection bias

• Assume (for simplicity) constant effects, \(Y_{1i}=Y_{0i} + \delta\)
• Since we don’t observe \(Y_{0}\) and \(Y_{1}\), we have to use the observed outcomes, \(Y_{i}\)

\[\begin{align} E[Y_{i} | D_{i}=1] &- E[Y_{i} | D_{i}=0] \\ =& E[Y_{1i} | D_{i}=1] - E[Y_{0i} | D_{i}=0] \\ =& \delta + E[Y_{0i} | D_{i}=1] - E[Y_{0i} | D_{i}=0] \\ =& \text{ATE } + \text{ Selection Bias} \end{align}\]

Selection bias

• Selection bias means \(E[Y_{0i} | D_{i}=1] - E[Y_{0i} | D_{i}=0] \neq 0\)
• In words, the potential outcome without treatment, \(Y_{0i}\), is different between those that ultimately did and did not receive treatment.
• e.g., treated group was going to be better on average even without treatment (higher wages, healthier, etc.)

Selection bias

• How to “remove” selection bias?
• How about random assignment?
• In this case, treatment assignment doesn’t tell us anything about \(Y_{0i}\) \[E[Y_{0i}|D_{i}=1] = E[Y_{0i}|D_{i}=0],\] such that \[E[Y_{i}|D_{i}=1] - E[Y_{i} | D_{i}=0] = \delta_{ATE} = \delta_{ATT} = \delta_{ATU}\]

Selection bias

• Without random assignment, there’s a high probability that \[E[Y_{0i}|D_{i}=1] \neq E[Y_{0i}|D_{i}=0]\]
• i.e., outcomes without treatment are different for the treated group

Omitted variables bias

• In a regression setting, selection bias is the same problem as omitted variables bias (OVB)
• Quick review: Goal of OLS is to find \(\hat{\beta}\) to “best fit” the linear equation \(y_{i} = \alpha + x_{i} \beta + \epsilon_{i}\)

Regression review

\[\begin{align} \min_{\beta} & \sum_{i=1}^{N} \left(y_{i} - \alpha - x_{i} \beta\right)^{2} = \min_{\beta} \sum_{i=1}^{N} \left(y_{i} - (\bar{y} - \bar{x}\beta) - x_{i} \beta\right)^{2}\\ 0 &= \sum_{i=1}^{N} \left(y_{i} - \bar{y} - (x_{i} - \bar{x})\hat{\beta} \right)(x_{i} - \bar{x}) \\ 0 &= \sum_{i=1}^{N} (y_{i} - \bar{y})(x_{i} - \bar{x}) - \hat{\beta} \sum_{i=1}^{N}(x_{i} - \bar{x})^{2} \\ \hat{\beta} &= \frac{\sum_{i=1}^{N} (y_{i} - \bar{y})(x_{i} - \bar{x})}{\sum_{i=1}^{N} (x_{i} - \bar{x})^{2}} = \frac{Cov(y,x)}{Var(x)} \end{align}\]

Omitted variables bias

• Interested in estimate of the effect of schooling on wages \[Y_{i} = \alpha + \beta s_{i} + \gamma A_{i} + \epsilon_{i}\]
• But we don’t observe ability, \(A_{i}\), so we estimate \[Y_{i} = \alpha + \beta s_{i} + u_{i}\]
• What is our estimate of \(\beta\) from this regression?

Omitted variables bias

\[\begin{align} \hat{\beta} &= \frac{Cov(Y_{i}, s_{i})}{Var(s_{i})} \\ &= \frac{Cov(\alpha + \beta s_{i} + \gamma A_{i} + \epsilon_{i}, s_{i})}{Var(s_{i})} \\ &= \frac{\beta Cov(s_{i}, s_{i}) + \gamma Cov(A_{i},s_{i}) + Cov(\epsilon_{i}, s_{i})}{Var(s_{i})}\\ &= \beta \frac{Var(s_{i})}{Var(s_{i})} + \gamma \frac{Cov(A_{i},s_{i})}{Var(s_{i})} + 0\\ &= \beta + \gamma \times \theta_{as} \end{align}\]

Removing selection bias without RCT

• The field of causal inference is all about different strategies to remove selection bias
• The first strategy (really, assumption) in this class: selection on observables or conditional indpendence

Intuition

• Example: Does having health insurance, \(D_{i}=1\), improve your health relative to someone without health insurance, \(D_{i}=0\)?
• \(Y_{1i}\) denotes health with insurance, and \(Y_{0i}\) health without insurance (these are potential outcomes)
• In raw data, \([Y_{i} | D_{i}=1] > E[Y_{i} | D_{i}=0]\), but is that causal?

Intuition

Some assumptions:

• \(Y_{0i}=\alpha + \eta_{i}\)
• \(Y_{1i} - Y_{0i} = \delta\)
• There is some set of “controls”, \(x_{i}\), such that \(\eta_{i} = \beta x_{i} + u_{i}\) and \(E[u_{i} | x_{i}]=0\) (conditional independence assumption, or CIA)

\[\begin{align} Y_{i} &= Y_{1i} \times D_{i} + Y_{0i} \times (1-D_{i}) \\ &= \delta D_{i} + Y_{0i} D_{i} + Y_{0i} - Y_{0i} D_{i} \\ &= \delta D_{i} + \alpha + \eta_{i} \\ &= \delta D_{i} + \alpha + \beta x_{i} + u_{i} \end{align}\]

ATEs versus regression coefficients

• Estimating the regression equation, \[Y_{i} = \alpha + \delta D_{i} + \beta x_{i} + u_{i}\] provides a causal estimate of the effect of \(D_{i}\) on \(Y_{i}\)
• But what does that really mean?

ATEs vs regression coefficients

• Ceteris paribus (“with other conditions remaining the same”), a change in \(D_{i}\) will lead to a change in \(Y_{i}\) in the amount of \(\hat{\delta}\)
• But is ceteris paribus informative about policy?

ATEs vs regression coefficients

• \(Y_{1i} = Y_{0i} + \delta_{i} D_{i}\) (allows for heterogeneous effects)
• \(Y_{i} = \alpha + \beta D_{i} + \gamma X_{i} + \epsilon_{i}\), with \(Y_{0i}, Y_{1i} \perp\!\!\!\perp D_{i} | X_{i}\)
• Aronow and Samii, 2016, show that: \[\hat{\beta} \rightarrow_{p} \frac{E[w_{i} \delta_{i}]}{E[w_{i}]},\] where \(w_{i} = (D_{i} - E[D_{i} | X_{i}])^{2}\)

ATEs vs regression coefficients

• Simplify to ATT and ATU
• \(Y_{1i} = Y_{0i} + \delta_{ATT} D_{i} + \delta_{ATU} (1-D_{i})\)
• \(Y_{i} = \alpha + \beta D_{i} + \gamma X_{i} + \epsilon_{i}\), with \(Y_{0i}, Y_{1i} \perp\!\!\!\perp D_{i} | X_{i}\)

\[\begin{align} \beta = & \frac{P(D_{i}=1) \times \pi (X_{i} | D_{i}=1) \times (1- \pi (X_{i} | D_{i}=1))}{\sum_{j=0,1} P(D_{i}=j) \times \pi (X_{i} | D_{i}=j) \times (1- \pi (X_{i} | D_{i}=j))} \delta_{ATU} \\ & + \frac{P(D_{i}=0) \times \pi (X_{i} | D_{i}=0) \times (1- \pi (X_{i} | D_{i}=0))}{\sum_{j=0,1} P(D_{i}=j) \times \pi (X_{i} | D_{i}=j) \times (1- \pi (X_{i} | D_{i}=j))} \delta_{ATT} \end{align}\]

ATEs vs regression coefficients

What does this mean?

• OLS puts more weight on observations with treatment \(D_{i}\) “unexplained” by \(X_{i}\)
• “Reverse” weighting such that the proportion of treated units are used to weight the ATU while the proportion of untreated units enter the weights of the ATT
• This is an average effect, but probably not the average we want