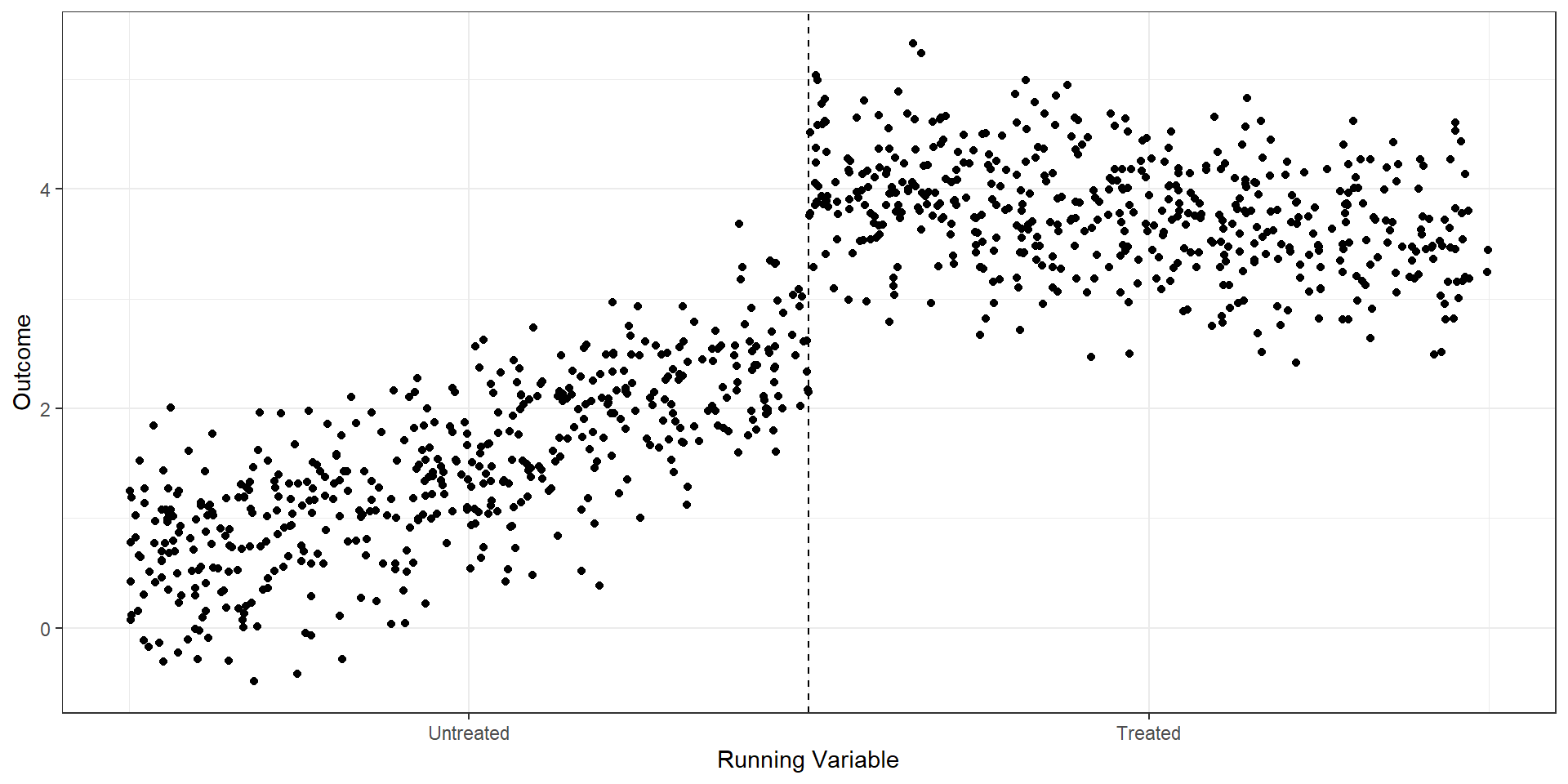
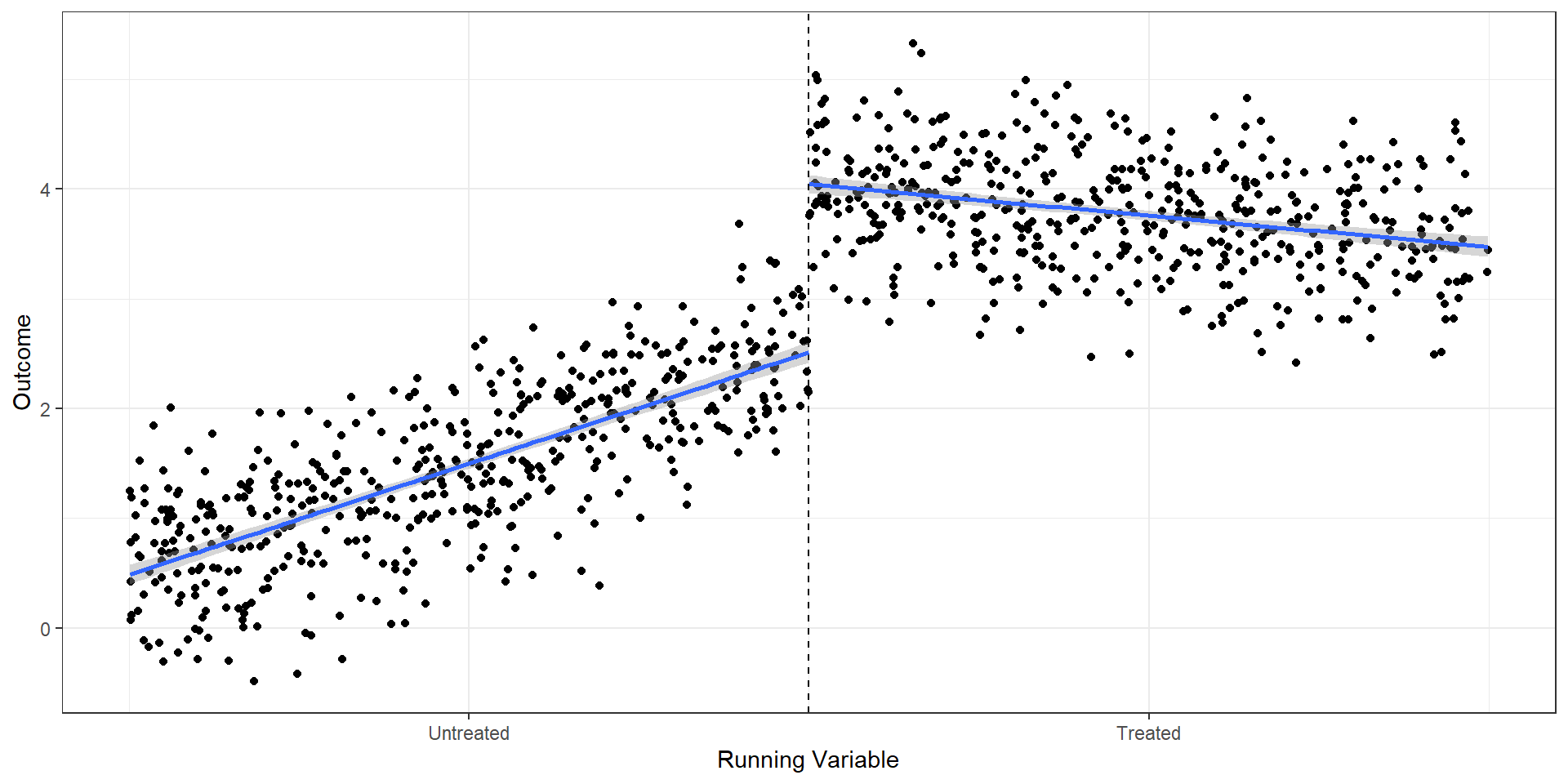
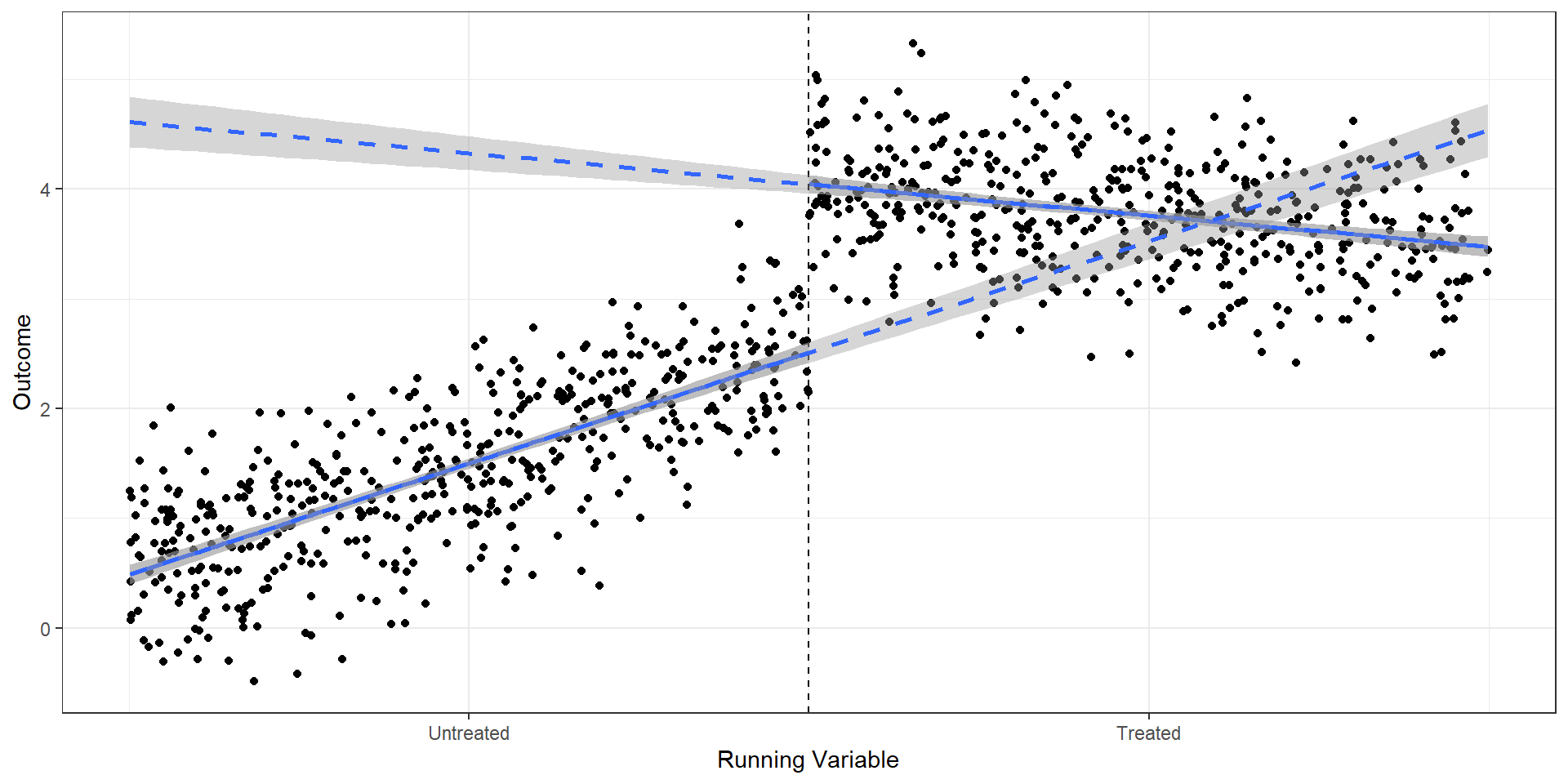
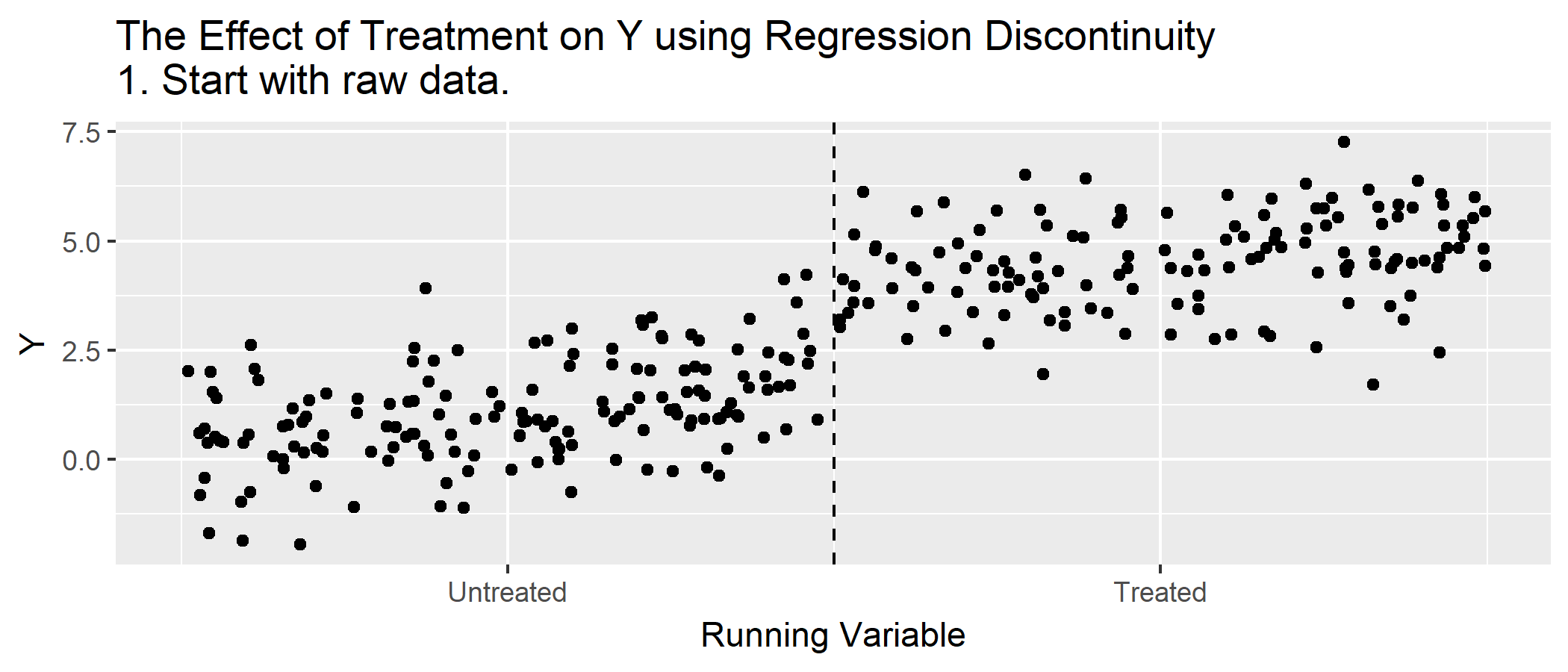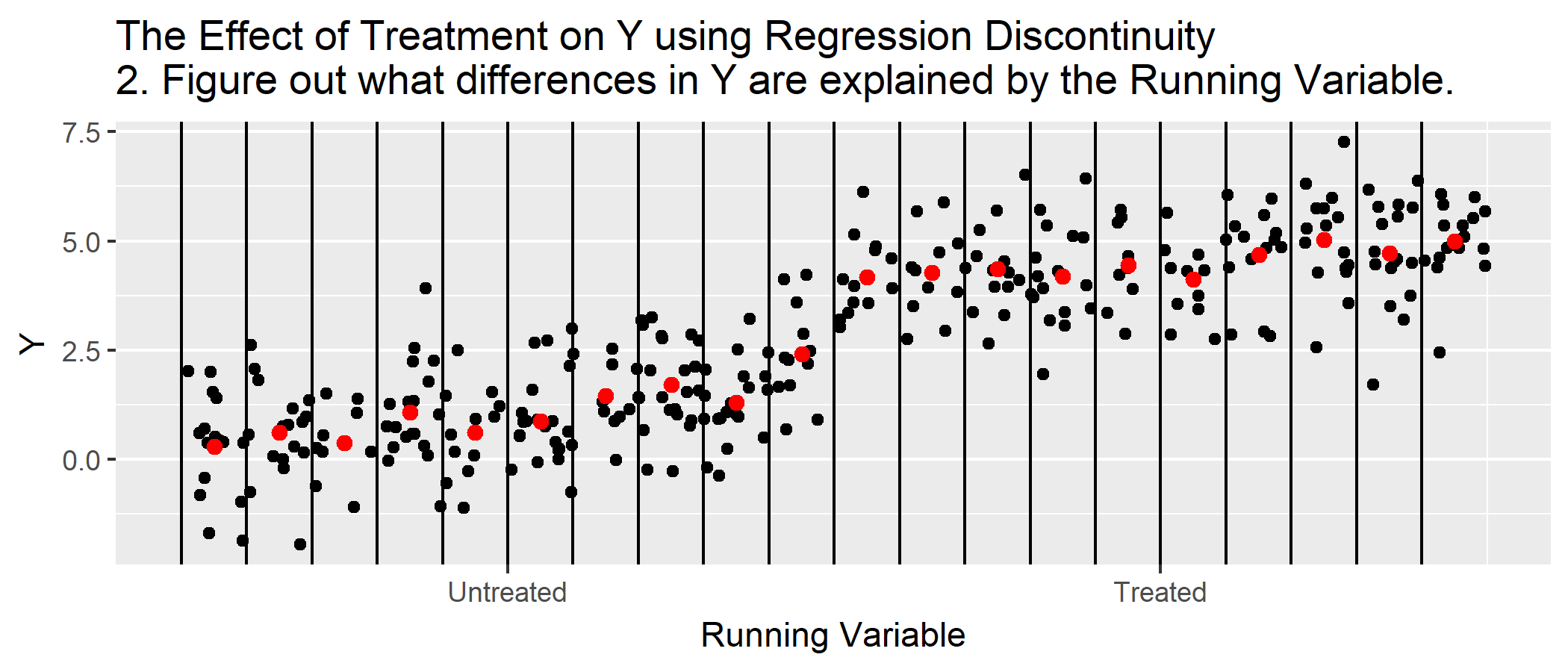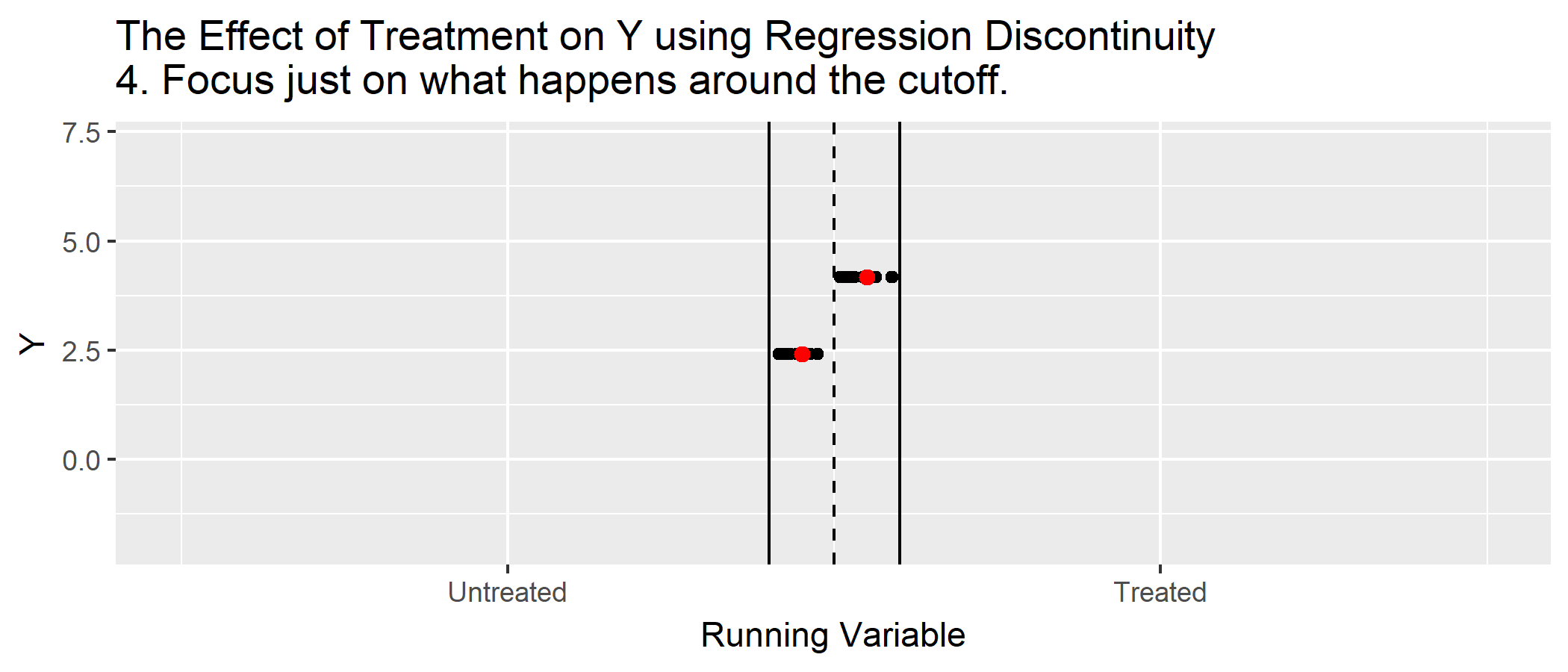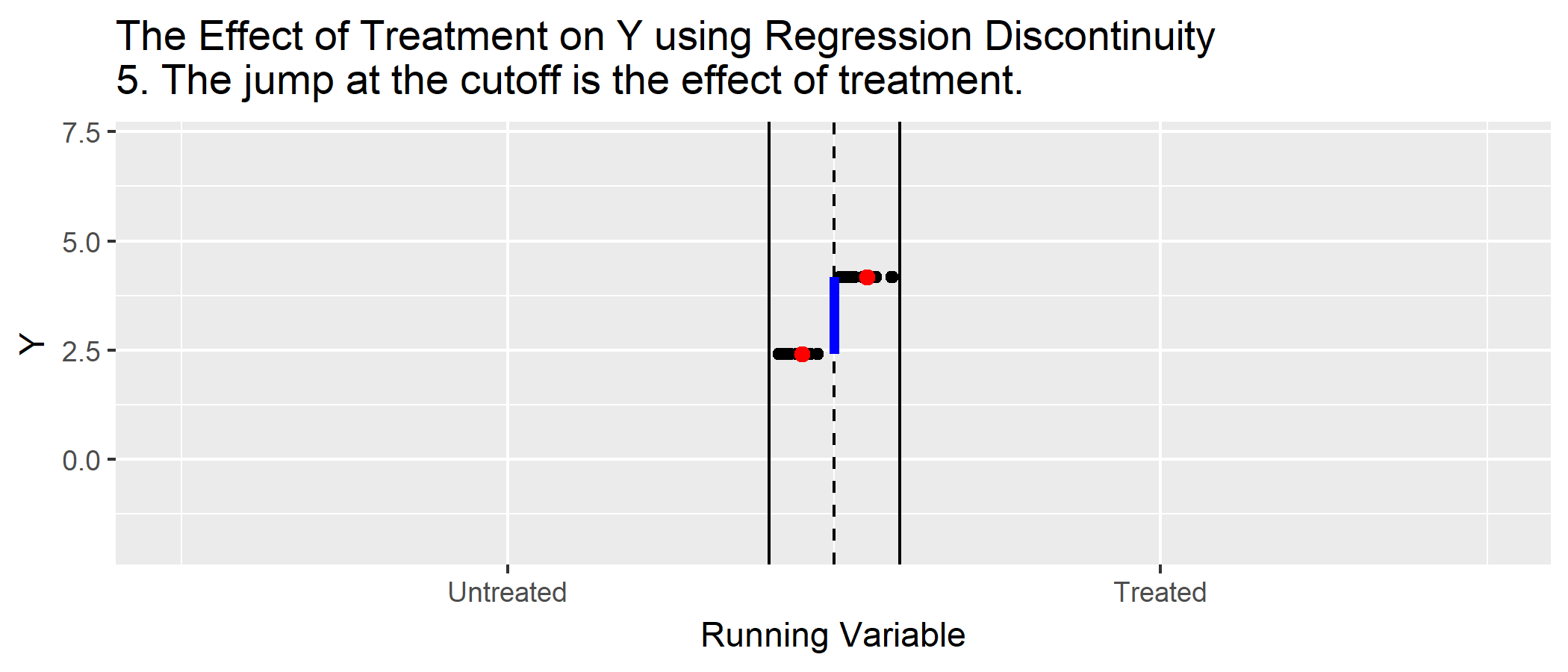
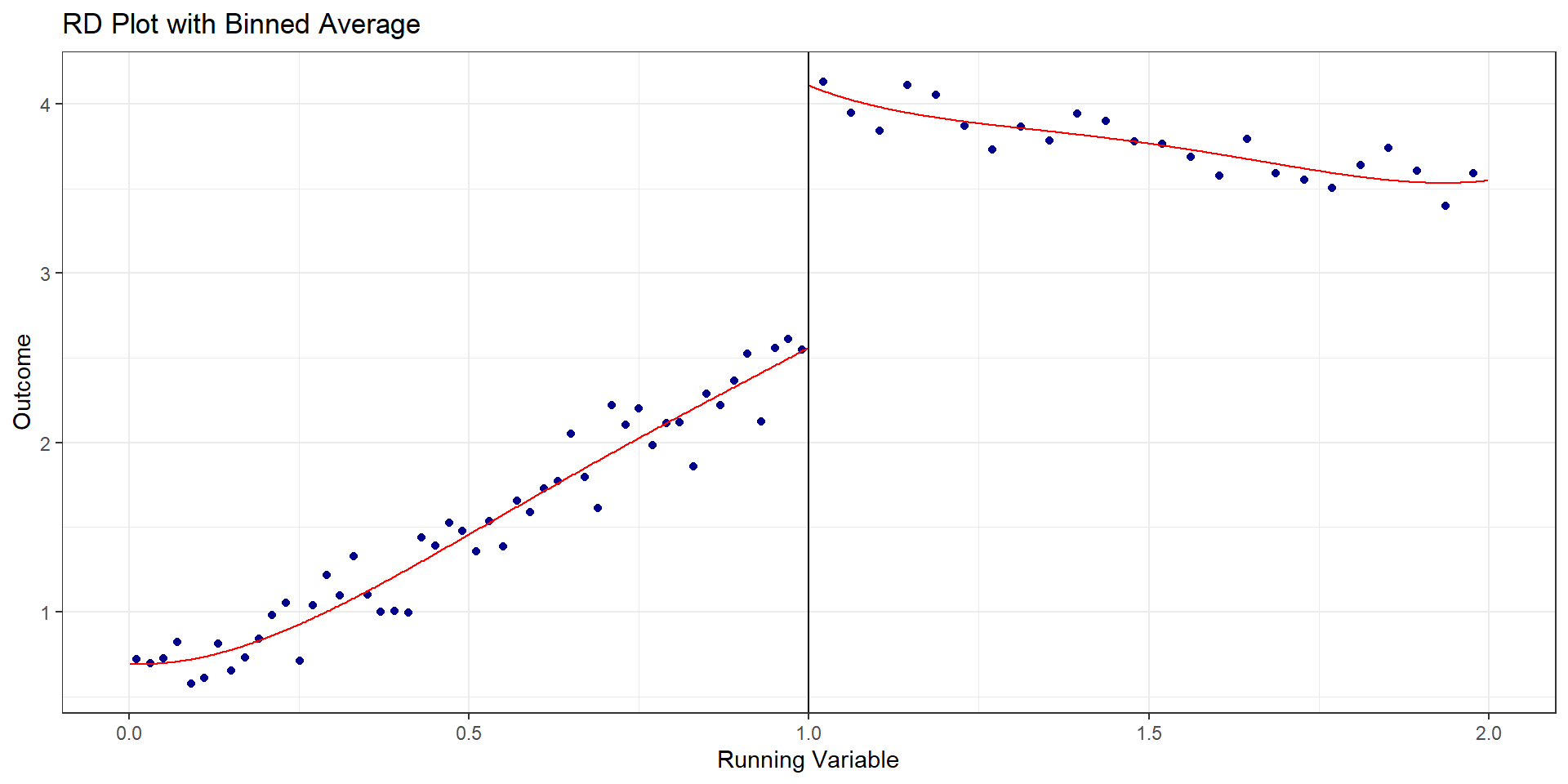
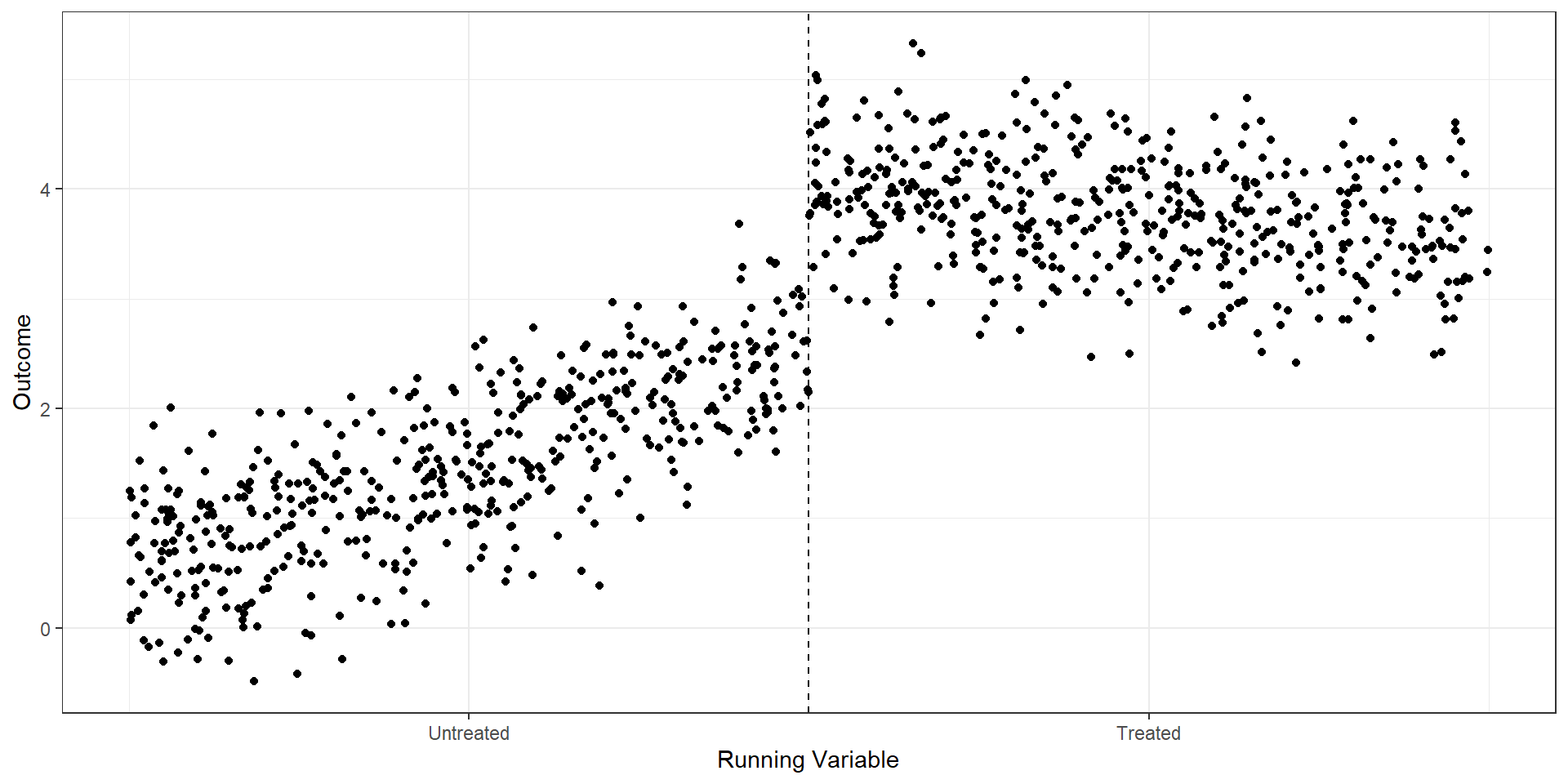
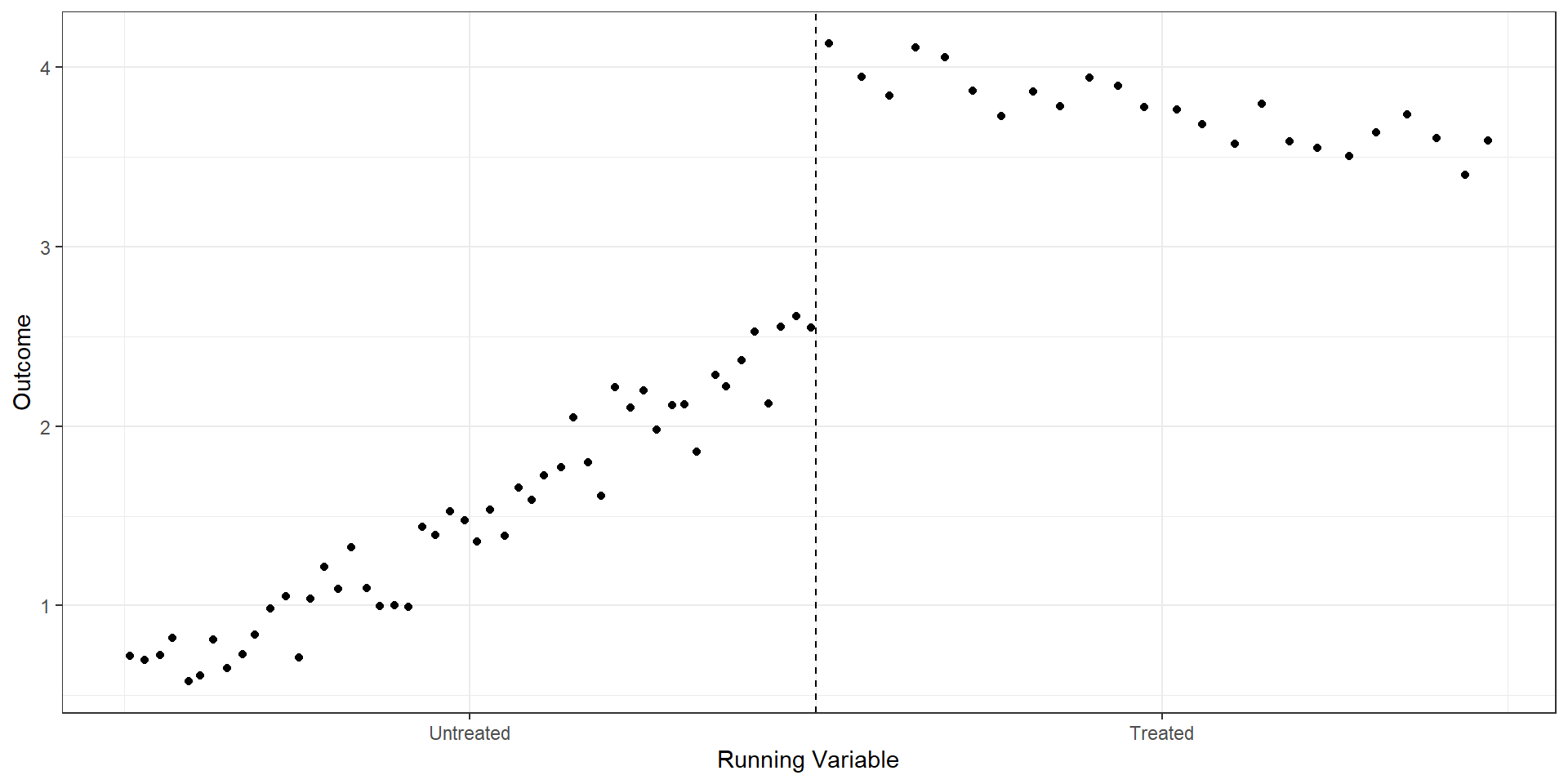
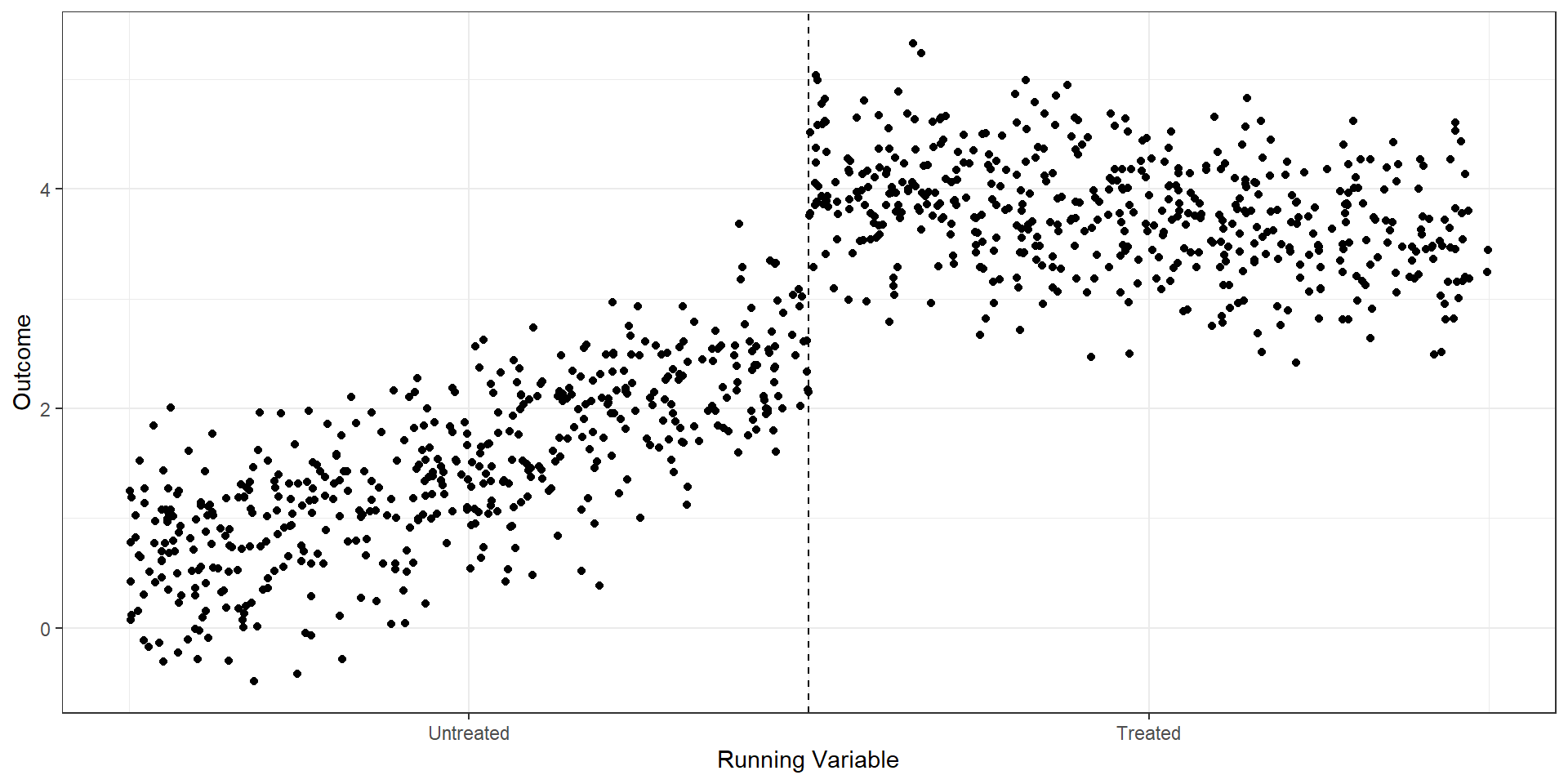
R Code
n=1000
rd.dat <- tibble(
X = runif(n,0,2),
W = (X>1),
Y = 0.5 + 2*X + 4*W + -2.5*W*X + rnorm(n,0,.5)
)
plot1 <- rd.dat %>% ggplot(aes(x=X,y=Y)) +
geom_point() + theme_bw() +
geom_vline(aes(xintercept=1),linetype='dashed') +
scale_x_continuous(
breaks = c(.5, 1.5),
label = c("Untreated", "Treated")
) +
xlab("Running Variable") + ylab("Outcome")
plot1