Understanding Difference-in-differences

Ian McCarthy | Emory University

Outline

  1. Panel Data and Fixed Effects
  2. Difference-in-Differences

Panel Data and Fixed Effects

Basics of panel data

  • Repeated observations of the same units over time (balanced vs unbalanced)
  • Identification due to variation within unit

Notation

  • Unit \(i=1,...,N\) over several periods \(t=1,...,T\), which we denote \(y_{it}\)
  • Treatment status \(D_{it}\)
  • Regression model,
    \(y_{it} = \delta D_{it} + \gamma_{i} + \gamma_{t} + \epsilon_{it}\) for \(t=1,...,T\) and \(i=1,...,N\)

Benefits of Panel Data

  • May overcome certain forms of omitted variable bias
  • Allows for unobserved but time-invariant factor, \(\gamma_{i}\), that affects both treatment and outcomes

Still assumes

  • No time-varying confounders
  • Past outcomes do not directly affect current outcomes
  • Past outcomes do not affect treatment (reverse causality)

Some textbook settings

  • Unobserved “ability” when studying schooling and wages
  • Unobserved “quality” when studying physicians or hospitals

Fixed effects and regression

\(y_{it} = \delta D_{it} + \gamma_{i} + \gamma_{t} + \epsilon_{it}\) for \(t=1,...,T\) and \(i=1,...,N\)

  • Allows correlation between \(\gamma_{i}\) and \(D_{it}\)
  • Physically estimate \(\gamma_{i}\) in some cases via set of dummy variables
  • More generally, “remove” \(\gamma_{i}\) via:
    • “within” estimator
    • first-difference estimator

Within Estimator

\(y_{it} = \delta D_{it} + \gamma_{i} + \gamma_{t} + \epsilon_{it}\) for \(t=1,...,T\) and \(i=1,...,N\)

  • Most common approach (default in most statistical software)

  • Equivalent to demeaned model: \[y_{it} - \bar{y}_{i} = \delta (D_{it} - \bar{D}_{i}) + (\gamma_{i} - \bar{\gamma}_{i}) + (\gamma_{t} - \bar{\gamma}_{t}) + (\epsilon_{it} - \bar{\epsilon}_{i})\]

  • \(\gamma_{i} - \bar{\gamma}_{i} = 0\) since \(\gamma_{i}\) is time-invariant

  • Requires strict exogeneity assumption (error is uncorrelated with \(D_{it}\) for all time periods)

First-difference

\(y_{it} = \delta D_{it} + \gamma_{i} + \gamma_{t} + \epsilon_{it}\) for \(t=1,...,T\) and \(i=1,...,N\)

  • Instead of subtracting the mean, subtract the prior period values \[y_{it} - y_{i,t-1} = \delta(D_{it} - D_{i,t-1}) + (\gamma_{i} - \gamma_{i}) + (\gamma_{t} - \gamma_{t-1}) + (\epsilon_{it} - \epsilon_{i,t-1})\]

  • Requires exogeneity of \(\epsilon_{it}\) and \(D_{it}\) only for time \(t\) and \(t-1\) (weaker assumption than within estimator)

  • Sometimes useful to estimate both FE and FD just as a check

Keep in mind…

  • Discussion only applies to linear case or very specific nonlinear models
  • Fixed effects at lower “levels” accommodate fixed effects at higher levels (e.g., FEs for hospital combine to form FEs for zip code, etc.)
  • Fixed effects can’t solve reverse causality
  • Fixed effects don’t address unobserved, time-varying confounders
  • Can’t estimate effects on time-invariant variables
  • May “absorb” a lot of the variation for variables that don’t change much over time

Within Estimator (Default) in practice

library(fixest)
library(causaldata)
reg.dat <- causaldata::gapminder %>%
  mutate(lgdp_pc=log(gdpPercap))
feols(lifeExp~lgdp_pc | country, data=reg.dat)

Within Estimator (Default) in practice

R Code 
library(fixest)
library(modelsummary)
library(causaldata)
reg.dat <- causaldata::gapminder %>%
  mutate(lgdp_pc=log(gdpPercap))
m1 <- feols(lifeExp ~ lgdp_pc | country, data=reg.dat)
modelsummary(list("Default FE"=m1), 
             shape=term + statistic ~ model, 
             gof_map=NA, 
             coef_rename=c("lgdp_pc"="Log GDP per Capita"))
Default FE
Log GDP per Capita 9.769
(0.702)

Within Estimator (Manually Demean) in practice

library(causaldata)
reg.dat <- causaldata::gapminder %>%
  mutate(lgdp_pc=log(gdpPercap)) %>%
  group_by(country) %>%
  mutate(demean_lifeexp=lifeExp - mean(lifeExp, na.rm=TRUE),
         demean_gdp=lgdp_pc - mean(lgdp_pc, na.rm=TRUE))
lm(demean_lifeexp~ 0 + demean_gdp, data=reg.dat)

Within Estimator (Manually Demean) in practice

R Code 
library(lmtest)
reg.dat <- causaldata::gapminder %>%
  group_by(country) %>%
  mutate(lgdp_pc=log(gdpPercap),
         lgdp_pc=lgdp_pc - mean(lgdp_pc, na.rm=TRUE),
         lifeExp=lifeExp - mean(lifeExp, na.rm=TRUE))

m2 <- lm(lifeExp~ 0 + lgdp_pc , data=reg.dat)
modelsummary(list("Default FE"=m1, "Manual FE"=m2), 
             shape=term + statistic ~ model, 
             gof_map=NA, 
             coef_rename=c("lgdp_pc"="Log GDP per Capita"),
             vcov = ~country)
Default FE Manual FE
Log GDP per Capita 9.769 9.769
(0.702) (0.701)

Note: feols defaults to clustering at level of FE, lm requires our input

First differencing (default) in practice

library(plm)
reg.dat <- causaldata::gapminder %>%
  mutate(lgdp_pc=log(gdpPercap))

plm(lifeExp ~ 0 + lgdp_pc, model="fd", individual="country", index=c("country","year"), data=reg.dat)

First differencing (manual) in practice

R Code 
library(plm)
reg.dat <- causaldata::gapminder %>%
  mutate(lgdp_pc=log(gdpPercap))

m3 <- plm(lifeExp ~ 0 + lgdp_pc, model="fd", index=c("country","year"), data=reg.dat)

modelsummary(list("Default FE"=m1, "Manual FE"=m2, "Default FD"=m3), 
             shape=term + statistic ~ model, 
             gof_map=NA, 
             coef_rename=c("lgdp_pc"="Log GDP per Capita"))
Default FE Manual FE Default FD
Log GDP per Capita 9.769 9.769 5.290
(0.702) (0.284) (0.291)

First differencing (manual) in practice

reg.dat <- causaldata::gapminder %>%
  mutate(lgdp_pc=log(gdpPercap)) %>%  
  group_by(country) %>%
  arrange(country, year) %>%
  mutate(fd_lifeexp=lifeExp - lag(lifeExp),
         lgdp_pc=lgdp_pc - lag(lgdp_pc)) %>%
  na.omit()

lm(fd_lifeexp~ 0 + lgdp_pc , data=reg.dat)

First differencing (manual) in practice

R Code 
reg.dat <- causaldata::gapminder %>%
  mutate(lgdp_pc=log(gdpPercap)) %>%  
  group_by(country) %>%
  arrange(country, year) %>%  
  mutate(fd_lifeexp=lifeExp - dplyr::lag(lifeExp),
         lgdp_pc=lgdp_pc - dplyr::lag(lgdp_pc)) %>%
  na.omit()

m4 <- lm(fd_lifeexp~ 0 + lgdp_pc , data=reg.dat)
modelsummary(list("Default FE"=m1, "Manual FE"=m2, "Default FD"=m3, "Manual FD"=m4), 
             shape=term + statistic ~ model, 
             gof_map=NA, 
             coef_rename=c("lgdp_pc"="Log GDP per Capita"))
Default FE Manual FE Default FD Manual FD
Log GDP per Capita 9.769 9.769 5.290 5.290
(0.702) (0.284) (0.291) (0.291)

FE and FD with same time period

R Code 
reg.dat2 <- causaldata::gapminder %>%
  mutate(lgdp_pc=log(gdpPercap)) %>%
  inner_join(reg.dat %>% select(country, year), by=c("country","year"))
m5 <- feols(lifeExp ~ lgdp_pc | country, data=reg.dat2)
modelsummary(list("Default FE"=m5, "Default FD"=m3, "Manual FD"=m4), 
             shape=term + statistic ~ model, 
             gof_map=NA, 
             coef_rename=c("lgdp_pc"="Log GDP per Capita"))
Default FE Default FD Manual FD
Log GDP per Capita 8.929 5.290 5.290
(0.741) (0.291) (0.291)

Don’t want to read too much into this, but…

  • Likely strong serial correlation in this case (almost certainly)
  • Mispecified model

Difference-in-Differences

Basic 2x2 Setup

Want to estimate \(ATT = E[Y_{1}(1)- Y_{0}(1) | D=1]\)

Pre-Period Post-Period
Treatment \(E(Y_{0}(0)|D=1)\) \(E(Y_{1}(1)|D=1)\)
Control \(E(Y_{0}(0)|D=0)\) \(E(Y_{0}(1)|D=0)\)


Problem: We don’t see \(E[Y_{0}(1)|D=1]\)

Basic 2x2 Setup

Want to estimate \(ATT = E[Y_{1}(1)- Y_{0}(1) | D=1]\)

Pre-Period Post-Period
Treatment \(E(Y_{0}(0)|D=1)\) \(E(Y_{1}(1)|D=1)\)
Control \(E(Y_{0}(0)|D=0)\) \(E(Y_{0}(1)|D=0)\)


Strategy 1: Estimate \(E[Y_{0}(1)|D=1]\) using \(E[Y_{0}(0)|D=1]\) (before treatment outcome used to estimate post-treatment)

Basic 2x2 Setup

Want to estimate \(ATT = E[Y_{1}(1)- Y_{0}(1) | D=1]\)

Pre-Period Post-Period
Treatment \(E(Y_{0}(0)|D=1)\) \(E(Y_{1}(1)|D=1)\)
Control \(E(Y_{0}(0)|D=0)\) \(E(Y_{0}(1)|D=0)\)


Strategy 2: Estimate \(E[Y_{0}(1)|D=1]\) using \(E[Y_{0}(1)|D=0]\) (control group used to predict outcome for treatment)

Basic 2x2 Setup

Want to estimate \(ATT = E[Y_{1}(1)- Y_{0}(1) | D=1]\)

Pre-Period Post-Period
Treatment \(E(Y_{0}(0)|D=1)\) \(E(Y_{1}(1)|D=1)\)
Control \(E(Y_{0}(0)|D=0)\) \(E(Y_{0}(1)|D=0)\)


Strategy 3: DD


Estimate \(E[Y_{1}(1)|D=1] - E[Y_{0}(1)|D=1]\) using \(E[Y_{0}(1)|D=0] - E[Y_{0}(0)|D=0]\) (pre-post difference in control group used to predict difference for treatment group)

Graphically

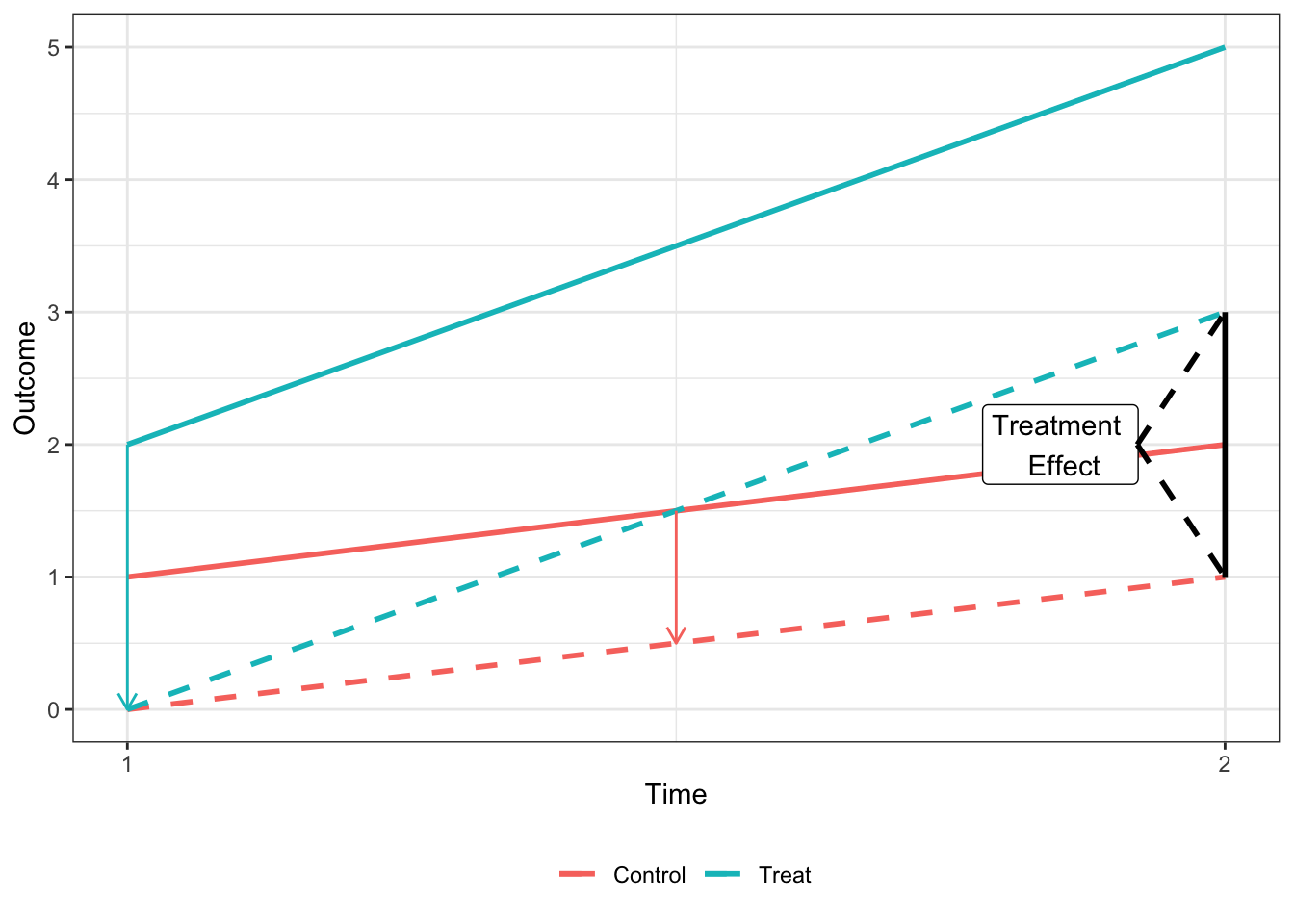
Basic DD Graph

Animations

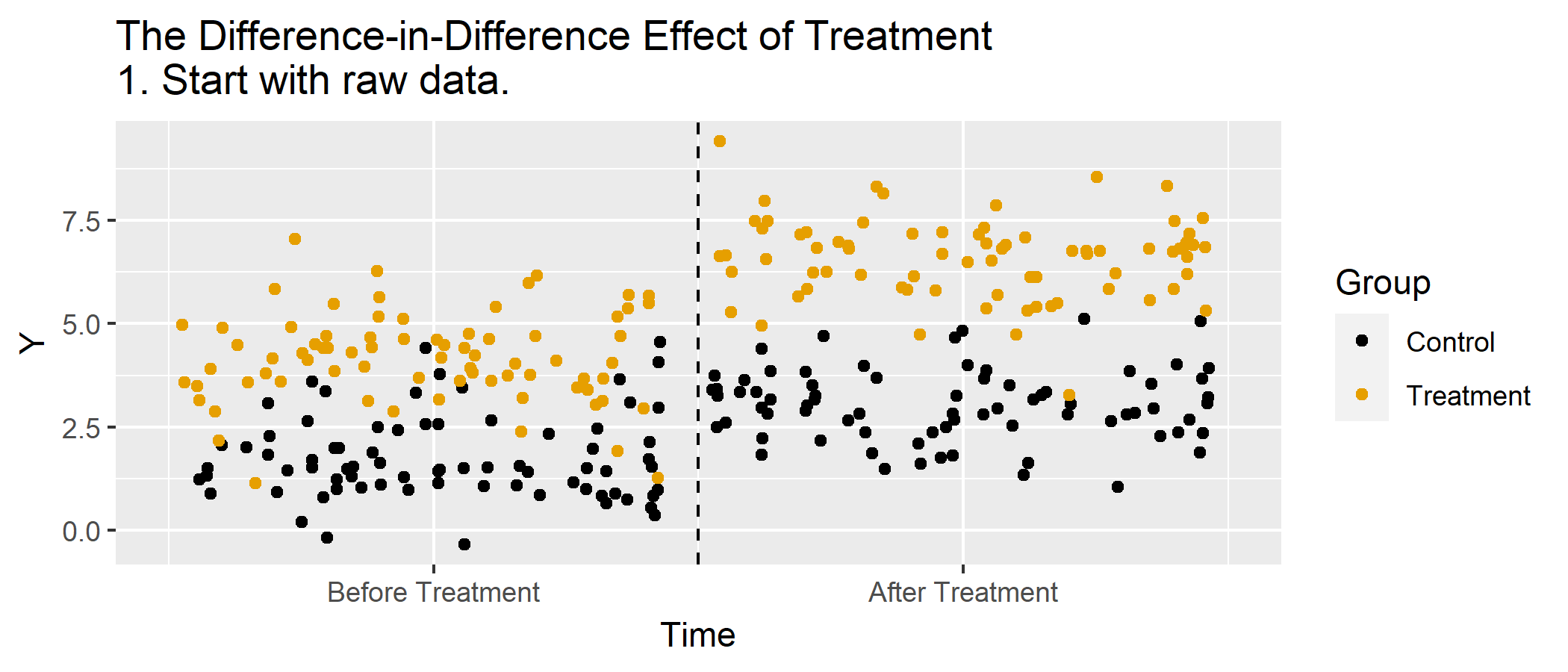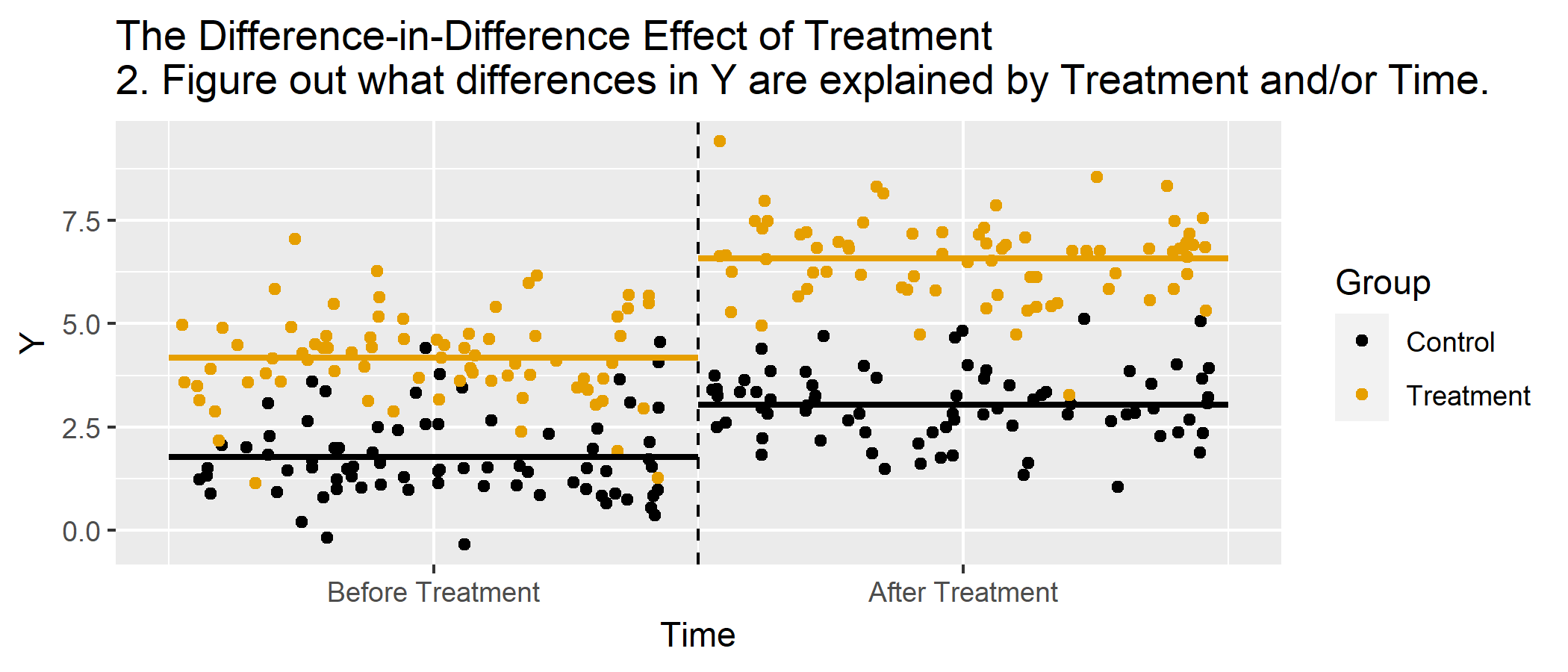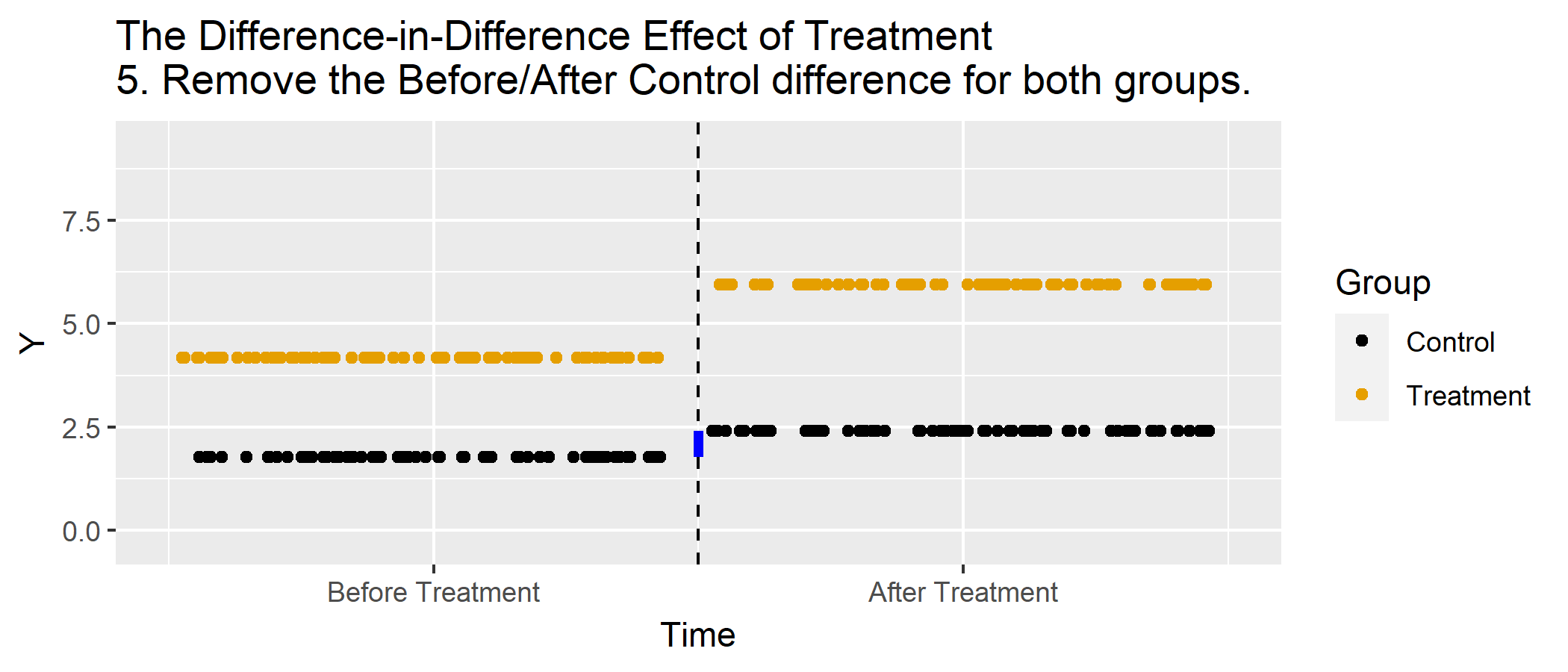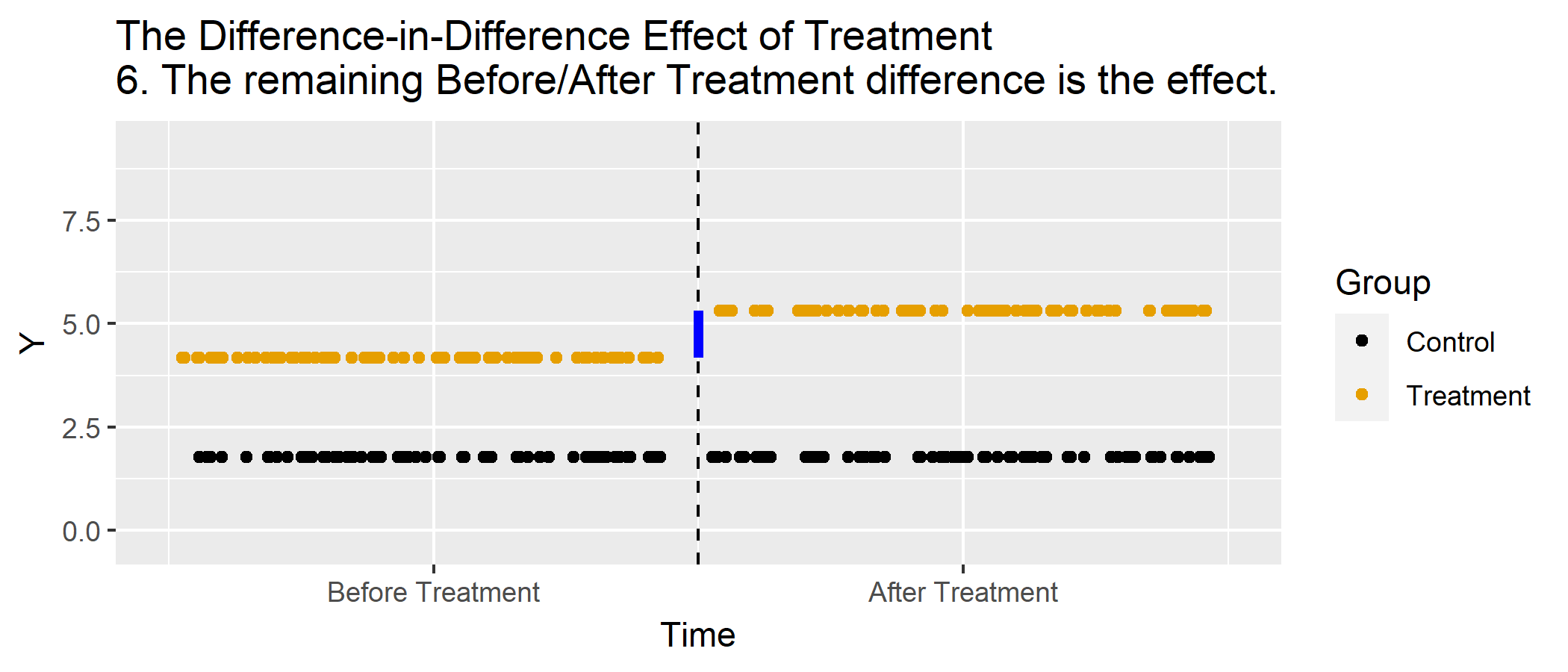
Basic DD Graph, Animated

ATE Estimates with DD

Key identifying assumption is that of parallel trends

\[E[Y_{0}(1) - Y_{0}(0)|D=1] = E[Y_{0}(1) - Y_{0}(0)|D=0]\]

Estimation: Sample Means

\[\begin{align} E[Y_{1}(1) - Y_{0}(1)|D=1] &=& \left( E[Y(1)|D=1] - E[Y(1)|D=0] \right) \\ & & - \left( E[Y(0)|D=1] - E[Y(0)|D=0]\right) \end{align}\]

Estimation: Regression

\[y_{it} = \alpha + \beta D_{i} + \lambda \times Post_{t} + \delta \times D_{i} \times Post_{t} + \varepsilon_{it}\]

Pre Post Post - Pre
Treatment \(\alpha + \beta\) \(\alpha + \beta + \lambda + \delta\) \(\lambda + \delta\)
Control \(\alpha\) \(\alpha + \lambda\) \(\lambda\)
Diff \(\beta\) \(\beta + \delta\) \(\delta\)

Simulated data

N <- 5000
dd.dat <- tibble(
  d = (runif(N, 0, 1)>0.5),
  time_pre = "pre",
  time_post = "post"
)

dd.dat <- pivot_longer(dd.dat, c("time_pre","time_post"), values_to="time") %>%
  select(d, time) %>%
  mutate(t=(time=="post"),
         y.out=1.5+3*d + 1.5*t + 6*d*t + rnorm(N*2,0,1))

Mean differences

R Code 
dd.means <- dd.dat %>% group_by(d, t) %>% summarize(mean_y = mean(y.out)) %>% mutate(d=ifelse(d==TRUE, "Treated", "Control"), t=ifelse(t==TRUE, "Post", "Pre"))

knitr::kable(dd.means, col.names=c("Treated","Period","Mean"), format="html")
Treated Period Mean
Control Pre 1.512192
Control Post 3.010816
Treated Pre 4.517785
Treated Post 12.026116

Mean differences

In this example:

  • \(E[Y(1)|D=1] - E[Y(1)|D=0]\) is 9.0152995
  • \(E[Y(0)|D=1] - E[Y(0)|D=0]\) is 3.0055927

So the ATT is 6.0097068

Regression estimator

R Code 
library(modelsummary)
dd.est <- lm(y.out ~ d + t + d*t, data=dd.dat)
modelsummary(dd.est, gof_map=NA, coef_omit='Intercept')
 (1)
dTRUE 3.006
(0.028)
tTRUE 1.499
(0.028)
dTRUE × tTRUE 6.010
(0.040)