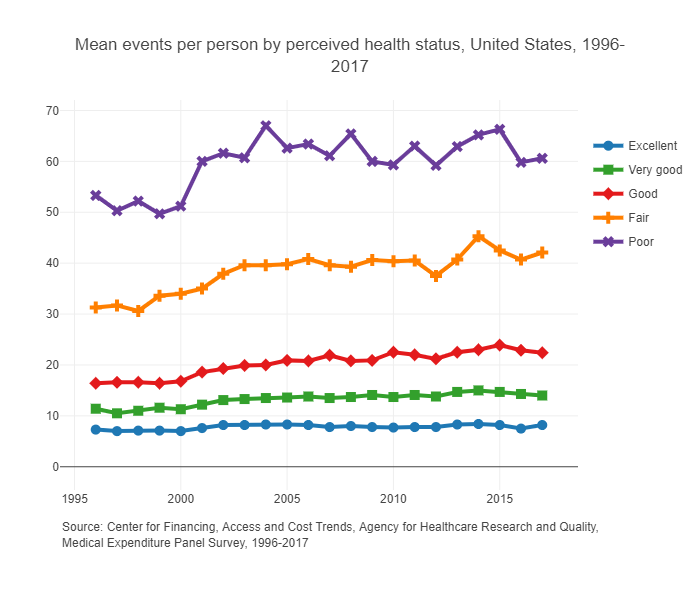
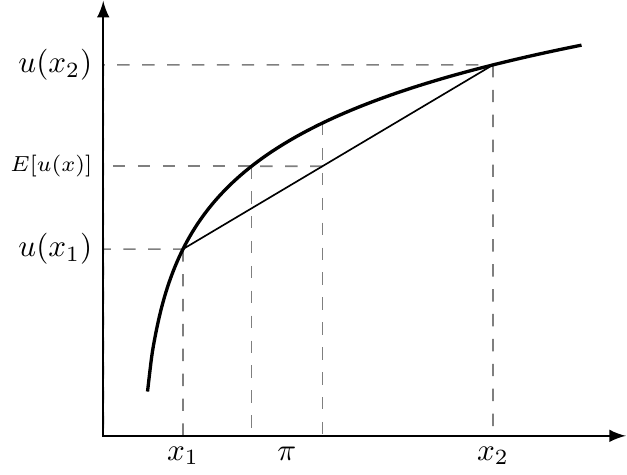
Example
Consider the utility function, \(u(w)=\ln(w)\). An individual starts with a wealth of $100,000. With probability 0.25, this person will get sick and incur a cost of $20,000.
- Calculate expected wealth, \(E[w]\).
- Calculate expected utility, \(E[U(w)]\).
- Calculate value of wealth that gives you \(u=E[U(w)]\) (based on the utility function).
- Calculate the risk premium as the difference between (1) and (3).
- Calculate maximum willingness to pay by adding the risk premium and the expected cost.
Answer
We’re asked to find some wealth level, \(y\), such that the person is indifferent between \(y\) with certainty versus the risky wealth levels, \(w_{h}=\) $100,000 with probability 0.75 or \(w_{s}=\) $80,000 with probability 0.25.
Expected wealth is: \(E[u]=0.75\times 100,000 + 0.25 \times 80,000 =\) 95,000
The person’s expected utility is: \(E[u]=0.75\times \ln (100000) + 0.25 \times \ln (80000) =\) 11.4571396.
We need \(y\) such that \(u(y)=\) 11.4571396. Given our utility function, this is satisfied for \(y=\) $94,574. This is the certainty equivalent.
The risk premium is then the expected wealth less the CE, or $ 425.84.
Since the person starts with $100,000, the full WTP for health insurance is $100,000 \(-\) $94,574 \(=\) $5,425.8, which is also the sum of the actuarily fair premium of $5,000 and the risk premium of $425.84.
In-class Problem: Demand for insurance
Assume that utility takes the log form, \(u(x)=ln(x)\). If someone is healthy, they maintain their current wealth of $100, and if they become ill, they must incur a cost of $50. Answer the following questions based on this setup.
- Calculate the risk premium and WTP based on a probability of illness of 0.1.
- Repeat part (1) using a probability of illness of 0.2.
- Repeat part (1) using a probability of illness of 0.5.
- Explain how these values differ and why. What might this say about the profitability of insurance in a market with many sick people?