Physician Agency and Financial Incentives
Physician Agency
- Basic idea: physicians strongly influence health care decisions, acting as agents on behalf of patients
- Potential for “other things” to influence care, including financial incentives
For the next couple of classes, we’re going to focus on the role of financial incentives. We’ll turn to the role of information barriers/heterogeneities at the end of this module
Do financial incentives matter?
Well…yes!
- Gruber and Owings, 1996. Physician Financial Incentives and Cesarean Section Delivery.
- Clemens and Gottlieb, 2014. Do Physician’s Financial Incentives Affect Medical Treatment and Patient Health.
With price setting power…
Setup
- Denote quantity of physician services by \(x\)
- Denote benefit of services to patient by \(B(x)\)
- Patients pay (and physicians receive) a price of \(p\) for each unit of service \(x\)
- Physicians incur cost \(c\) for each unit of care
- Net benefit to patients is \(NB(x)=B(x)-px\)
- Physicians must choose quantity of care at least better than the patient’s outside option, \(NB(x)= B(x)-px \geq NB^{0}\).
Solving the model
- With this framework, how much care will be provided? (i.e., what is the optimal value of \(x\))
- Solve the model in two steps:
- Physician will provide minimum surplus to keep the patient, \(NB(x) = B(x)-px = NB^{0}\)
- Substitute into physician profit function, \(\pi=(p-c)x = B(x)-NB^{0} - cx\), and solve for \(x\)
In-class Problem: Physician agency
Denote the quantity of care consumed by \(x\), and denote by \(B(x)\) the function that determines the benefit of care to the patient. Assume that the patient must pay the full price of care, \(px\), so that their net benefit is \(NB=B(x)−px\). Further assume that the physician can choose both \(x\) and \(p\).
- Find the patient’s optimal \(x\).
- Draw the marginal benefit function on a graph and note the price and patient’s optimal quantity. Assume that \(B'(x)>0\) and \(B''(x)<0\) (i.e., the marginal benefit function is positive and downward sloping).
- Find the physician’s optimal \(x\) assuming \(NB^{0}=0\).
- Add the physician’s optimal \(x\) to your graph and interpret the difference.
Physician agency in a graph
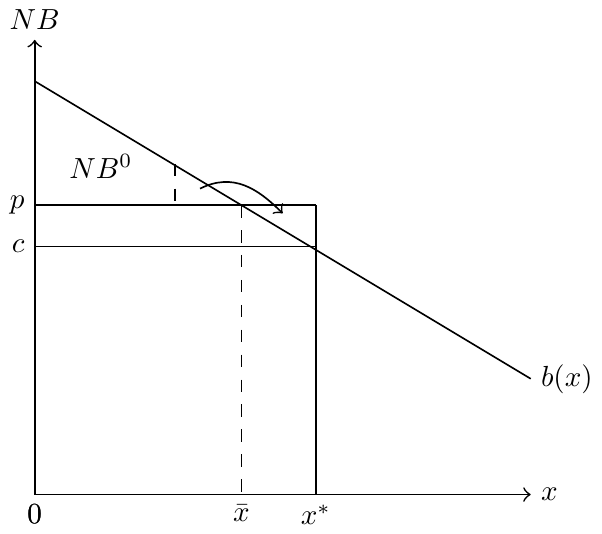
Depiction of physician agency
Example
Assume \(B(x)=8x^{1/2}\), \(NB^{0}=2\), and \(c=1\):
- Find the physician’s optimal level of \(x\) and \(p\).
- Find the patient’s optimal level of \(x\).
- Draw this graphically.
Answer
First let’s re-write the constraint such that \(px = 8x^{1/2}\) and \(\pi = 8x^{1/2} - 2 - x\). The first order condition for \(x\) is then \(4x^{-1/2} -1 =0\), which is satisfied at \(x^{*}=16\). Substituting this into the constraint, \(8x^{1/2} - px=2\) yields \(p=\frac{15}{8}\).
But if they could choose on their own, the patient would prefer to maximize their net benefit. This would occur at \(4x^{-1/2}=p\), which yields \(x=(32/15)^{2} \approx 4.5\) at \(p=15/8\).
With fixed prices…
Solving the model
The two step approach applies when prices and quantity of care are variable. If the physician cannot set price, then we just work off of the constraint, \(B(x)-\bar{p}x=NB^{0}\).
Why? This is a corner solution…can’t just take a derivative.
In-class Problem: Agency and fixed prices
Assume \(B(x)=4x^{1/2}\), \(NB^{0}=0\), anc \(c=1\). Further assume that prices are fixed administratively at, \(\bar{p}=2\). Note that, in this case, we work only off of the patient’s net benefit constraint.
- What is the physician’s and patient’s optimal amount of care provided?
- The government is considering increasing the price to \(\bar{p}=3\). What are the new optimal levels of care for physicians and patients at this new price?
- How would the price change affect the difference between the patient and physician’s optimal amounts?
Comparative statics
An increase in the administratively set price leads to a decrease in quantity of services provided. And vice versa, a reduction in price leads to an increase in quantity provided. Why?
\[\begin{align*} b(x)\frac{\mathrm{d}x}{\mathrm{d}p} - x - p\frac{\mathrm{d}x}{\mathrm{d}p} &= 0 \\ \frac{\mathrm{d}x}{\mathrm{d}p} = \frac{-x}{p-b(x)} &< 0. \end{align*}\]
Comparative statics
- This comes from the physician’s constraint, which is essentially a reflection of demand
- Higher \(\bar{p}\) means the constraint is met at a lower value of \(x\), and vice versa
Why does this matter?
- Say we want to reduce health care utilization, and we try to do so by cutting payments. Will this work?
- Relevant for current policy, Axios Article
Takeaways
- Basic model of physician agency and financial incentives
- Focus on role of financial incentives, but clearly other dimensions worth studying
