Unilateral Pricing
Motivation
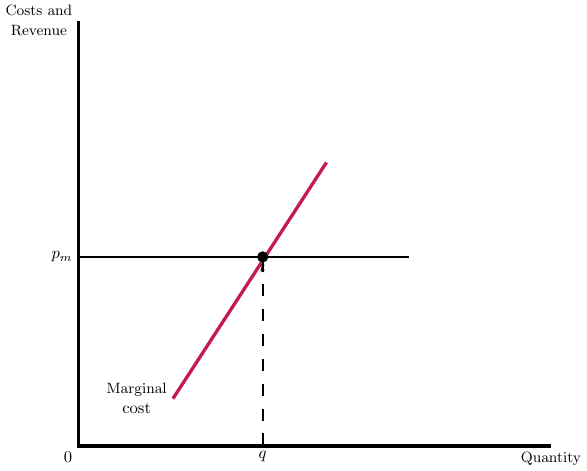
In health care, providers usually face two prices:
- A price fixed by Medicare and Medicaid, \(p_{m}\).
- A price that is negotiated with insurers, \(p_{n}\).
How does \(p_{m}\) affect \(p_{n}\)? For now, let’s focus on these two situations separately.
Unilateral Pricing (depends on the objective)
Pricing for NFP hospitals
Objective is to maximize some function of profits and quantity of care provided, denoted by \[U\left( \pi_{j} = \pi_{i,j} + \pi_{g,j},D_{i,j}, D_{g,j} \right)\]
where \(\pi_{j}\) denotes total profits for hospital \(j\) and \(D_{i,j}\) denotes hospital demand from insurer \(i\). We assume that \(p_{j}\) is exogenous and determined by a public payer, so the hospital need only set its price for private insurance customers, \(p_{i}\).
Solution for NFP hospital
The hospital chooses \(p_{i}\) such that
\[\frac{\mathrm{d}U}{\mathrm{d}p_{i}} = U_{1} \pi_{1}^{i} + U_{2} \frac{\mathrm{d}D_{i}}{\mathrm{d}p_{i}}=0\]
where \(U_{1}\) denotes the derivative of \(U(\cdot)\) with respect to its first argument and similarly for \(U_{2}\).
In general, we can’t solve this directly without knowing the hospital’s utility function.
Assuming pure profit maximization
Example
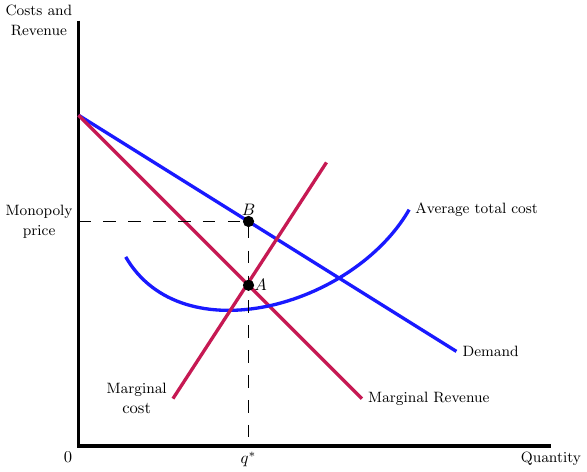
Consider the firm’s demand curve, \(d=16-q\), and cost curve, \(c(q)=5+q^{2}\). Where will the firm produce and at what price? What is the firm’s markup over marginal cost?
The profit function is, \(\pi = (16-q)q - 5 - q^{2}\). Differentiating with respect to quantity yields \(-q + 16 - q - 2q= 16-4q=0\), or \(q=4\). At this quantity, the price is \(p=12\), which is a markup of 4 over the marginal cost (or 50% markup).
In-class problem (unilateral pricing)
Consider the firm’s demand curve, \(d=40-2q\), and cost curve, \(c(q)=5q+\frac{1}{2}q^{2}\).
- What is the firm’s profit maximizing choice of quantity and price?
- What is the markup over marginal cost?
Pure Price Taker
Sell at the public price to the point where marginal revenue equals marginal cost