Brand Name Drugs

Ian McCarthy | Emory University

Pricing for Brand Name Drugs

Price?

Recall, “price” is confusing in pharma
Price to wholesaler, to pharmacy, to insurer, to patient
Significant (and opaque) rebates throughout the supply chain

From Manufacturer’s Perspective

Economics of pricing for brand name drugs:

Unique, patent-protected drug with no close substitutes (Monopoly)
Many products with patent protection and imperfect substitutes (Bertrand differentiated products)

Monopoly Pricing

Some examples

Lipitor (lifetime revenue of over $130 billion)
Humira (lifetime revenue of over $100 billion)
Advair (lifetime revenue of over $90 billion)

Monopoly pricing without insurance

Inverse demand, $p=a-b*q$
Costs, $FC + c*q$
Profits, $\pi = (a-c)q - bq^2 - FC$

Profit maximizing choice of $p, q$:

$q^* = \frac{a-c}{2b}$
$p^* = \frac{a+c}{2}$

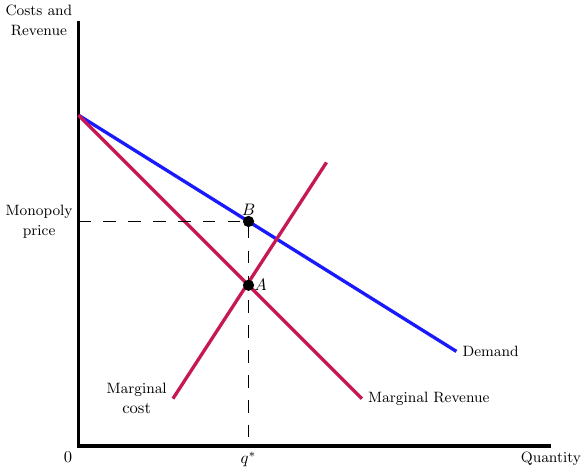
Depiction of monopoly pricing

Monopoly pricing with insurance

If insurers set co-insurance rates and copays based on a fixed price, then it wouldn’t matter much
But…the supply price will vary depending on the form of cost sharing
Need to consider pricing under coinsurance versus copayments separately

Monopoly pricing with coinsurance

Denote coinsurance by $\alpha$, with $\alpha \in (0,1)$
For price $p$, patient pays $\alpha \times p$ and insurer pays $(1-\alpha) \times p$
Willingness to pay is unchanged, so new inverse demand curve is $p = \frac{1}{\alpha}*(a - b*q)$
Acts as a rotation of demand, with new slope $\frac{1}{\alpha} \times b$ (steeper demand curve, less elastic)

Monopoly pricing with coinsurance

New profit maximizing choice of $p, q$:

$q^{*} = \frac{a-\alpha c}{2b}$
$p^{*} = \frac{1}{2} (\frac{a}{\alpha}+c)$

Comparison of monopoly pricing

Monopoly price is higher with coinsurance than without
To see this, let’s take the ratio of prices with and without coinsurance:

\[\frac{p^{*}_{c}}{p^{*}_{nc}} = \frac{\frac{1}{2} (\frac{a}{\alpha}+c)}{\frac{a+c}{2}} = \frac{1}{\alpha}\]

Monopoly pricing with copayments

Recall copayment is a fixed amount paid by the patient
With demand price fixed and independent of supply price, seller can set any price to insurer
Coinsurance penalizes high prices by working down demand curve, but copayments do not
Coinsurance shifts burden of price increases directly onto patients and confers downward price pressure relative to case of copayments

Real world example

Speciality drugs more likely to be unique, with few close substitutes
Theoretical prediction: coinsurance should be more common with specialty drugs versus more common drugs
Empirical evidence: coinsurance rates increasing for specialty drugs over time, 25% in 2006 to 33% in 2009

Bertrand Differentiated Products

Setup

Many partial (but imperfect) substitute products with market power
Akin to brand name drug (i.e., with patent protection) with some substitutes
Simplify to 2 drugs from two companies:
- Denote demand for drug 1 by $q_{1}(p_{1},p_{2})$
- Denote demand for drug 2 by $q_{2}(p_{1},p_{2})$
- $\frac{d q_{i}}{d p_{j}} > 0$, so that products are substitutes
- $\frac{d q_{i}}{d p_{i}} < 0$, as usual (downward sloping demand)

Specific Bertrand Setup

Players: Firm 1 and Firm 2
Actions: Each firm chooses a price $p_{i}$ for its product.
Demand: The demand for firm $i$’s product: \[q_{i} = a - bp_{i} + cp_{j}\]
Profits: Each firm’s profit: \[\pi_{i} = (p_{i} - mc_{i})q_{i}\]

Key Points:

$a$ is the maximum quantity when the price is zero
$b$ represents how quantity demanded changes with the product’s price
$c$ captures the effect of the rival firm’s price on demand

Best Response Functions

Firm 1: \[p_{1}^*(p_{2}) = \frac{a + cp_{2} + mc_{1}}{2b + 1}\] Firm 2: \[p_{2}^*(p_{1}) = \frac{a + cp_{1} + mc_{2}}{2b + 1}\]

Key Points:

Each firm’s price is a function of the other firm’s price
Best response functions represent the optimal price choice in response to the rival’s price

Nash Equilibrium

Equating the two best response functions to solve for equilibrium prices:

\[\begin{align*} p_{1}^* &= \frac{a(2b+1) + c(a + mc_{2}) + mc_{1}(2b+1)}{2b+1 - c^2} \\ p_{2}^* &= \frac{a(2b+1) + c(a + mc_{1}) + mc_{2}(2b+1)}{2b+1 - c^2} \end{align*}\]

Key Points:

Nash equilibrium prices are where neither firm has an incentive to change its price unilaterally
Both firms maximize their profit given the other firm’s price

Comparison to Monopoly Pricing

Monopoly Price (previously derived): \[p_{m} = \frac{a + mc_{m}}{2b}\]

Comparison:

Classical Monopoly vs. Competition: Monopolists set higher prices than competitive firms
Differentiation: In Bertrand, differentiation can lead to prices closer to monopoly levels, depending on the substitution effect (parameter $c$)
Cost Structures: Bertrand prices depend on both firms’ costs; monopoly price only depends on its own cost

Bertrand Pricing with Insurance

Stage 1: Insurer chooses one drug with copayment $c$ to be on formulary. Other drug will not be covered at all
Stage 2: Bertrand pricing with “bids” to insurer
Stage 3: Insurer selects drug to be on formulary

Solution Idea

Imagine firm 1 set price to original bertrand price, $p_{1}^{b}$
Firm 2 can then set price to $p_{2}^{b}=p_{1}^{b}-\epsilon$ and get most or all of the market
So, $p_{1}^{b}, p_{2}^{b}$ is not an equilibrium
Firms lower price until extra sales on formularly are less than profit of drug off formulary
Final prediction: Insurers used tiered formularies and copayments for differentiated (but substitutable) on-patent drugs

Summary from joint hearings in FTC and DOJ

Unique drugs with patent protection:

Under these circumstances, there is little opportunity for a purchaser to stimulate competition among manufacturers. Manufacturers are roughly free to set launch prices, they rarely discount those prices, and purchasers and price takers.

Differentiated drugs with imperfect substitutes:

This stage represents the lion’s share of the market at any given time…Depending on how similar the drugs are…organized purchasers have the ability to either switch patients in a medially appropriate way…or at least start new patients on a preferred drug…This is the area where formularies can be applied for the greatest effect on overall costs.